1 2 Следующая > 

Доверительные интервалы

Решения задач с 2001 по 2050

Задача 2001. Из 7000 вкладчиков банка по схеме случайной бесповторной выборки было отобрано 250 вкладчиков. Средний размер вклада в выборке составил 700 руб., а среднеквадратическое отклонение 210 руб. Какова вероятность того, что средний размер вклада случайно выбранного вкладчика отличается от его среднего размера в выборке не более чем на 35 руб. (по абсолютной величине)?

Задача 2002. В N-ской области проведено исследование возраста 100 случайно выбранных работников государственных предприятий.
возраст, лет 15-25 25-35 35-45 45-55 55-65
число работников 6 24 37 22 11
С доверительной вероятностью 0,95 найти доверительный интервал среднего возраста работников государственных предприятий N-ской области в предположении, что возраст работников распределен нормально.

Задача 2003. Взято 16 проб молока, поступивших на реализацию из акционерного сельскохозяйственного предприятия. Средняя жирность молока составила 3,7% при среднем квадратическом отклонении 0,5%. Какова вероятность того, что средняя жирность молока всех партий не выйдет за пределы от 3,6% до 3,8%?

Задача 2004. По данным 17 сотрудников фирмы, где работает 220 человек, среднемесячная заработная плата составила 320 у.е., при S=72 у.е. Какая минимальная сумма должна быть на счету фирмы, чтобы с вероятностью γ=0,98 гарантировать выдачу заработной платы всем сотрудникам?

Задача 2005. Из 300 предприятий решено по схеме собственно случайной бесповторной выборке было отобрано 100 предприятий. Распределение их по размеру годовой прибыли характеризуется следующими значениями.
Годовая прибыль 10-20 20-30 30-40 40-50 50-60 Свыше 60 итого
Млн. руб. 4 12 36 24 16 8 100
Найти:
А) границы, в которых с вероятностью 0,9901 заключена средняя годовая прибыль всех предпринимателей.
Б) Вероятность того, что доля всех предприятий, годовая прибыль которых менее 40 млн. руб. отличается от доли таких предприятий в выборке не более чем на 0,05 (по абсолютной величине).
В) Объём бесповторной выборки, при которой те же границы для средней годовой прибыли предприятий (смотри пункт А) можно гарантировать с вероятностью 0,95.

Задача 2006. Для нахождения среднего времени прорастания семян из большой партии по схеме собственно-случайной бесповторной выборки было отобрано 200 семян. Распределение семян по времени их прорастания представлено в таблице:
Время прорастания, дни менее 4 4-6 6-8 8-10 10-12 12-14 более 14 Итого
Число семян 2 14 55 73 38 10 8 200
Найти:
А) границы, в которых с вероятностью 0,9011 находится среднее время прорастания семян по всей партии;
Б) вероятность того, что доля семян во всей партии, прорастающих менее 8 дней, отличается от доли таких семян в выборке не более чем на 0,1 (по абсолютной величине).
В) объем выборки, при которой те же границы для среднего времени прорастания семян (см. п. а)) можно гарантировать с вероятностью 0,9643.

Задача 2007. Выборочная совокупность образуется для определения средней продолжительности горения электрической лампочки. Какой должен быть объём повторной выборки, чтобы с вероятностью 0,98 предельная ошибка не превзошла 40 часов. Генеральное среднее квадратичное отклонение равно 120 часов.

Задача 2008. Для отрасли, включающей 11000 фирм, была составлена случайная выборка из 55 фирм. По выборочным данным оказалось, что в фирме работают в среднем 77,5 человек при среднем квадратическом отклонении 10 человек. Пользуясь 95%-ным доверительным интервалом, оцените среднее число работающих в фирме по всей отрасли и общее число работающих в отрасли.

Задача 2009. Для определения токсической дозы яд был введен 30 мышам, 8 из которых погибли. Определить границы доверительного интервала для вероятности того, что данная доза окажется смертельной, при доверительной вероятности 0,95, предполагая, что число смертельных исходов в данном опыте подчиняется биномиальному закону распределения.

Задача 2010. Обследование оплаты труда n=300 колхозников дало следующие результаты: 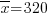рублей и S=15 рублей. В предположении о нормальной генеральной совокупности определить число колхозников, оплата труда которых находится в интервале от 310 рублей до 330 рублей.

Задача 2011. Менеджер компании, занимающейся прокатом автомобилей, оценивает среднюю величину пробега одного автомобиля в течение месяца. Из 380 автомобилей компании с помощью бесповторной выборки отобрано 32 автомобиля. Установлено, что средний пробег автомобиля составляет 1300 км, со стандартным отклонением 100 км. Найти 99,9% доверительный интервал, покрывающий средний пробег автомобилей всего парка в течение месяца.

Задача 2012. Средняя урожайность пшеницы на 20 опытных участках области составила х=25.0 ц/га, а S = 2ц/га. Найти:
а) с надежностью 0,975 границы доверительного интервала для оценки генеральной средней;
б) в предположении о нормальном распределении вероятность того, что среднеквадратическое отклонение генеральной совокупности находиться в интервале (0,9S; 1,1S).

Задача 2013. Для определения средней урожайности поля площадью 1800 га взято на выборку по 1 кв.м с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 6. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более, чем на 0.25 ц.

Задача 2014. Произведено 5 равноточных измерений расстояния от орудия до цели одним прибором со средним квадратическим отклонением случайных ошибок измерений σ=40м. Найти доверительный интервал для оценки истинного расстояния до цели с надежностью γ= 0,95, зная среднее арифметическое результатов измерений 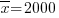м.

Задача 2015. В целях изучения среднедушевого дохода семей в 2000 году была произведена 2% выборка из 17 тысяч семей. По результатам обследования среднедушевой доход семьи составил 11 тысяч рублей, со среднеквадратическим отклонением, равным 7 тысяч рублей. Найти 99,73% доверительный интервал, покрывающий неизвестный генеральный среднедушевой доход, генеральная совокупность подчинена нормальному закону распределения.

Задача 2016. Производится обследование на предмет среднего времени просмотра телепередач с 8 до 14 часов. Каким должен быть объем выборки, чтобы отклонение выборочной средней от генеральной не превышало 5 минут (по абсолютной величине) с вероятностью 0,95? Если в предыдущих исследованиях средне стандартное отклонение времени просмотра передач составило 20 минут.

Задача 2017. Для определения потерь зерна при уборке случайным способом проведено 100 измерений. Средняя величина потерь составила 1,8ц с одного гектара посевов, при среднем квадратичном отклонении 0,5ц с га. С доверительной вероятностью 0,95 определить границы в которых будет находиться средняя величина потерь зерна с 1га и возможная величина потерь, если площадь уборки зерновых составила 640га. Долей выборки пренебречь.

Задача 2018. По данным выборочного обследования жирности молока (16 проб) средняя жирность молока равна 3,8% при дисперсии 0,64. Найти предельную ошибку выборки для средней жирности молока с вероятностью 0,9. Долю выборки пренебречь, а для 1,ф принять значение 1,75.

Задача 2019. Найти доверительный интервал, накрывающий с надежностью 0,95 неизвестное значение числа «нестандартных» проб воды в коммунальных водопроводах, если отмечено превышение концентрации различных токсических веществ в следующих количествах проб на 100 случайно отобранных: 12, 13, 12, 10, 11, 12, 14, 12, 11, 13.

Задача 2020. Автомат фасует рис в пакеты так, что все пакетов риса является нормально распределенной случайной величиной со стандартным отклонением σ=10 г. Произведена случайная выборка объемом n=40 пакетов. Средний вес пакета риса в выборке оказался равен 910 г. Найдите доверительный интервал для среднего веса пакета риса в генеральной совокупности с доверительной вероятностью p=0,99.

Задача 2021. На обувной фабрике изготавливают детские сапоги одного размера. По выборке объема 50 вычислена выборочная средняя длина подошвы сапог 19,8. Найти с надежностью 0,99 доверительный интервал для средней длины a подошвы сапога, если известно, что среднее квадратическое отклонение длин равно σ=0,1. Предполагается, что длины подошв распределены нормально.

Задача 2022. Для определения скорости расчетов с кредиторами предприятий была проведена случайная выборка десяти платежных документов, по которым срок перечисления денег оказался равным: 20 25 26 28 30 27 30 24 29 31 (дней).
С помощью доверительного интервала оценить с надежностью γ=0,95 ожидаемый срок перечисления и получения денег кредиторами (математическое ожидание), считая генеральную совокупность нормально распределенной.

Задача 2023. Коммерческий банк, изучая возможности предоставления долгосрочных кредитов населения, опрашивает своих клиентов для определения среднего размера такого кредита. Из 9706 клиентов банка опрошено 1000 человек. Среднее значение необходимого клиенту кредита в выборке составило 6750 у.е. со стандартным отклонением 1460 у.е. Найдите границы 95%-ого доверительного интервала для оценки неизвестного среднего значения кредита в генеральной совокупности.

Задача 2024. При подсчёте количества листьев у одного из лекарственных растений были получены следующие данные: 8,10,7,9,11,6,9,8,10,7. Найти вероятность, с которой доверительный интервал шириной равной 2 накрывает истинное значение параметра.

Задача 2025. При 12-кратном измерении температуры раствора серной кислоты получены следующие значения: 20.0, 20.3, 20.0, 20.2, 19.5,20.5, 19.7, 20.0, 19.6, 19.8. Дать точечную и интервальную (с доверительной вероятностью, равной 0,95) оценки истинной концентрации раствора, а так же оценить относительную погрешность измерения концентрации.

Задача 2026. Выборочное исследование деятельности коммерческих банков региона показало, что в среднем каждый банк имеет 14 филиалов в регионе (со стандартным отклонением, равным 8). Найти объем выборки, позволивший сделать такую оценку, если предельная ошибка оценки генеральной средней находится в пределах 20% от ее выборочного среднего значения, а доверительная вероятность составляет 0,95.

Задача 2027. На фармацевтическом заводе вычислили средний объем наполнения 100 ампул, отобранных по схеме собственно случайной бесповторной выборки. Он оказался равным 1,25 см, а дисперсия 0,01. Найти границы, в которых с вероятностью 0,9973 заключен средний объем выпускаемых фармацевтическим заводом ампул.

Задача 2028. Имеются данные о продаже швейных товаров по кварталам некоторых периодов: 396; 438; 398; 412; 414; 422; 436; 418; 413; 474; 450; 418; 412; 480; 478; 519; 429; 437; 391; 368.
Рассчитать гарантийный запас товара на квартал с надежностью 0,96. План – 460.

Задача 2029. Профсоюзный комитет по выборке из 6 предприятий отрасли подсчитал, что в среднем 3% рабочего времени оплачивается по листам нетрудоспособности со среднеквадратичным отклонением в 0,5%. Найти доверительный интервал для среднего процента рабочего времени, оплачиваемого по листам нетрудоспособности с надежностью 0,95; 0,98.

Задача 2030. На контрольных испытаниях 17 электроламп найдено, что средний срок службы лампы равен 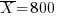часов при S=100. Определите нижнюю границу срока службы с доверительной вероятностью 0,95.

Задача 2031. Для определения урожая на корню озимой пшеницы было наложено в разных частях поля в случайном порядке 5 метровок и определено, соответственно, 5 показателей урожайности (в пересчете на ц/га): 35,3; 34,9; 35,2; 34,8; 34,8.
Необходимо:
1) дать точечную оценку генеральной средней урожайности, генеральной дисперсии и генерального среднего квадратического отклонения;
2) определить доверительный интервал для генеральной средней с вероятностью 0,95;
3) определить вероятность, что ошибка выборочной средней не превысит 0,1 ц/га;
4) необходимый объем выборки (количество наложенных метровок), чтобы с вероятностью 0,99 гарантировать ошибку выборки не более 0,1ц/га.

Задача 2032. Из большой партии обуви было отобрано случайно 800 штук для определения средней продолжительности носки. Среднее арифметическое полученной выборки 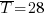месяцев. Найти с доверительной вероятностью 0,98 доверительный интервал для средней продолжительности носки обуви во всей партии, если среднее квадратичное отклонение продолжительности носки равно 4 месяца.

Задача 2033. По данным выборочных обследований в 1995 г. Прожиточный минимум населения Северо-Кавказского района составил в среднем на душу населения 87 тыс. руб. в месяц. Каким должен был быть минимально необходимый объем выборки, чтобы с вероятностью 0,997 можно было утверждать, что этот показатель уровня жизни населения в выборке отличается от своего значения в генеральной совокупности не более чем на 10 тыс. руб., если среднее квадратическое отклонение принять равным 30 тыс. руб.?

Задача 2034. С целью изучения размеров дневной выручки в сфере мелкого бизнеса была произведена 10%-ная случайная бесповторная выборка из 1000 торговых киосков города. В результате были получены данные о средней дневной выручке, которая составила 500 руб. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка всех торговых точек изучаемой совокупности, если среднее квадратичное отклонение составило 150 руб?

Задача 2035. При проверке веса импортируемого груза на таможне методом случайно повторной выборки было отобрано 200 изделий и в результате был установлен средний вес изделия 28 грамм при среднем квадратическом отклонении 4 грамма. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.

Задача 2036. Произведено 30 измерений диаметров деталей. По результатам измерений найдено среднее значение диаметров 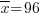мм. Предположив, что ошибки измерения распределены по нормальному закону распределения со средним квадратическим отклонением σ = 0,5 мм, найти вероятность того, что параметр генеральной совокупности a будет находиться внутри доверительного интервала со случайными границами (0,999 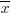; 1,001 )

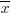Задача 2037. Станок-автомат штампует валики. По выборке объема n=100 вычислено выборочное математическое ожидание a (в сантиметрах) диаметра валика. Найти с надежностью 0,99 точность δ, с которой выборочное математическое ожидание оценивает математическое ожидание диаметра валика, зная что их среднее квадратическое отклонение &sigma=2 мм. Предполагается, что диаметры валиков распределены нормально.

Задача 2038. С целью изучения размеров выручки киосков была произведена 10%-ая случайная бесповторная выборка из 1000 киосков города. В результате были получены данные о средней выручке составившие 500 у.е. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка, если среднее квадратическое отклонение составило 150 у. е.?

Задача 2039. На овцеводческой ферме из стада произведена выборка для взвешивания 36 овец. Их средний вес оказался равным 50 кг. Предположив распределение веса нормальным, и определив несмещенную оценку выборочной дисперсии - 16, найти доверительный интервал для оценки математического ожидания с надежностью 0,9 веса.

Задача 2040. На заводе, где работают 10 тыс. рабочих, необходимо определить их средний стаж работы. Предварительным обследованием установлено, что среднее квадратическое отклонение стажа работы равно 5 годам. Определить необходимую численность выборки при условии, что с вероятностью 0,97 ошибка выборочной средней не превысит 1 года.

Задача 2041. Коммерческий банк, изучая возможности предоставления долгосрочных кредитов населению, опрашивает своих клиентов для определения среднего размера такого кредита. Из 9700 клиентов банка опрошено 1000 человек. Среднее значение необходимого кредита в выборке составило 7750 у.е. со стандартным отклонением 1560 у.е. Найдите границы 95%-ного доверительного интервала для оценки неизвестного среднего значения кредита в генеральной совокупности.

Задача 2042. В результате проведенных пяти измерений частоты пульса у больного получены следующие значения: 70, 90, 100, 80, 90. При доверительной вероятности 0,95 найти интервальную оценку частоты пульса у больного.

Задача 2043. Из партии объемом 500 однородных товаров для проверки по схеме случайной бесповторной выборки отобрано 70 товаров, среди которых оказалось 56 небракованных. Найдите вероятность того, что доля бракованных товаров во всей партии отличается от полученной доли в выборке не более чем на 0,02 (по абсолютной величине), а также границы, в которых с надежностью 0,96 заключена доля бракованных товаров во всей партии.

Задача 2044. Для исследования доходов населения города, составляющего 20 тыс. человек, по схеме собственно-случайной бесповторной выборки было отобрано 1000 жителей. Получено следующее распределение жителей по месячному доходу:
Месячный доход, руб Менее 500 500-1000 1000-1500 1500-2000 2000-2500 Свыше2500
Количество человек 58 96 239 328 147 132

1) Найти вероятность того, что средний месячный доход жителя города отличается от среднего дохода его в выборке не более, чем на 45 руб. ( по абсолютной величине)
2) Определит границы, в которых с вероятностью 0,99 заключен средний месячный доход жителей города;
3) Каким должен быть объем выборки, чтобы те же границы гарантировать с надежностью 0, 9973?

Задача 2045. По предварительному опросу населения большого города, в котором участвовало 900 жителей, за мероприятие Х готовы проголосовать 400 человек из опрошенных жителей. Найти 90%-ый доверительный интервал, в котором находится истинный процент готовых проголосовать за мероприятие Х.

Задача 2046. Из проверяемых на всхожесть 8000 зерен случайным образом отобрано 1000. Среди них оказалось 89% недоброкачественных. Найти доверительную вероятность того, что процент таких зерен в генеральной совокупности отличается от их процента в выборке не более, чем на 2% (по абсолютной величине). Рассмотреть случаи повторной и бесповторной выборки.

Задача 2047. С целью размещения рекламы опрошено 420 телезрителей, из которых данную передачу смотрят 170 человек. С доверительной вероятностью γ=0,91 найти долю телезрителей, охваченных рекламой в лучшем случае.

Задача 2048. Из большой партии электромагнитных реле было отобрано и подвергнуто контрольной проверке 600 шт. Среди них 18 шт. оказалось дефектными. Определить вероятность того, что во всей партии доля бракованных реле окажется не меньше 0.01 и не более 0.05.

Задача 2049. Для оценки вероятности появления дефектов были обследованы детали, выпускаемые некоторой производственной линией. Среди них было обнаружено дефектных деталей. Построить доверительный интервал для истинной вероятности появления дефектной детали с доверительной вероятностью, равной 0,95. n=49; k=9

Задача 2050. Из партии объемом 500 однородных товаров для проверки по схеме случайной бесповторной выборки отобрано 80 товаров, среди которых оказалось 64 небракованных. Найдите вероятность того, что доля бракованных товаров во всей партии отличается от полученной доли в выборке не более чем на 0,02 (по абсолютной величине), а также границы, в которых с надежностью 0,96 заключена доля бракованных товаров во всей партии.

1 2 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.