< Предыдущая 1 ... 21 22 23 24 25 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 13192 по 13246

Задача 13192. На АТС могут поступать вызовы трех типов. Вероятности поступления 1-го, 2-го и 3-го типа соответственно равны 0,2, 0,3, 0,5. По условиям задачи события, состоящие в поступлении вызова, независимые. Поступило три вызова. Какова вероятность того, что: а) все они разных типов, б) среди них нет вызова 1-го типа?

Задача 13194. Вероятность попадания в цель первого стрелка – 0,85, второго – 0,745, третьего – 0,63. Найти вероятность того, что цель поражена.

Задача 13195. Система состоит из двух приборов: основного и дублирующего. Вероятность безотказной работы основного прибора системы равна 0,9, а дублирующего прибора – 0,8. При выходе основного прибора из строя происходит мгновенное переключение системы на дублирующий прибор. Определить вероятность безотказной работы системы.

Задача 13196. Из множества чисел 000, 001, …, 999 наудачу выбирают одно число. Найдите вероятность того, что это число не содержит 1, если известно, что все его цифры различны.

Задача 13197. Для производственной практики 30 студентам предоставлены 15 мест в Москве, 8 мест - в Туле и 7 - в Воронеже. Какова вероятность того, что два определенных студента попадут на практику в один город?

Задача 13198. Над изготовлением изделия работают последовательно трое рабочих. Качество изделия при передаче следующему рабочему не проверяется. Первый рабочий допускает брак с вероятностью 0,1, второй – 0,2, третий – 0,05. Найти вероятность того, что при изготовлении изделия будет допущен брак.

Задача 13199. По цели производится 3 выстрела. Даны события Аi — попадание в цель при i выстреле (i = 1,2,3). Выразить через Аi и следующие события: В0 — ни одного попадания в цель; В1 — хотя бы одно попадание в цель.

Задача 13200. Три стрелка стреляют по мишени. Вероятность попадания в цель для первого стрелка равна 0,5; для второго — 0,6 и для третьего — 0,7. Найти вероятность того, что в результате однократного выстрела всех трех стрелков по мишени в ней будет: а) одна пробоина; б) хотя бы одна пробоина.

Задача 13201. Машина дает продукцию, которая должна удовлетворять определенным требованиям. Вероятность того, что данная единица продукции приемлема, составляет 95%. Из продукции машины делают выборку в количестве 10 ед. Какова вероятность того, что все 10 единиц продукции окажутся приемлемыми?

Задача 13202. Двадцати пяти студентам предоставлено для производственной практики 10 мест в Барнауле, 8 – в Хабаровске и 7 – в Томске. Найти вероятность того, что три друга попадут в один город.

Задача 13203. В урне 2 белых шара и 4 черных. Производится следующий опыт: из урны наудачу извлекают один шар, и если этот шар черный, то опыт прекращают, если же он белый, то шар возвращают в урну и добавляют еще два белых шара, после чего, по такой же схеме повторяют испытания. Найдите вероятность того, что в опыте будет выполнено 20 испытаний.

Задача 13204. Три станка работают независимо друг от друга. Вероятность того, что потребует наладки I станок, равна 0,2; II станок – 0,3; III станок – 0,1. Вычислить вероятность того, что ровно один станок потребует наладки; хотя бы один станок потребует наладки, не менее двух потребуют наладки.

Задача 13205. Несколько раз бросают игральную кость. Какова вероятность того, что одно очко появится впервые при N бросании? N=3

Задача 13206. В урне 6 черных, 5 красных шаров. Какова вероятность того, что выпадет 3 шара в последовательности: черный, красный, черный.

Задача 13207. Вероятность того, что в течение года обанкротится первое предприятие, равна 0.1 , второе – 0.05, третье – 0.01. Найти вероятность того, что в течение года обанкротится только одно предприятие.

Задача 13208. Наудачу подбрасывают 3 игральных кости. Пусть А - событие состоящее в том, что на верхней грани хотя бы одной из костей выпали 6 очков, а В - событие, состоящее в том, что на верхних гранях костей выпали разные количества очков. Найти Р(А|B), Р(В|А).

Задача 13209. В двух партиях 87% и 31% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:
А) хотя бы одно изделие бракованное,
Б) два бракованных,
В) одно доброкачественное и одно бракованное.

Задача 13210. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок, равна 0,7, второй – 0,75, третий – 0,8. Найти вероятность того, что в течение смены внимания рабочего потребуют не менее двух станков.

Задача 13211. В электрическую цепь включены параллельно два прибора. Вероятность отказа первого прибора равна 0,1, второго 0,2. Найти вероятность того, что откажет хотя бы один прибор этой цепи.

Задача 13212. В двух ящиках находятся детали: в 1-ом – 10 (из них 3 стандартных), во 2-ом – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.

Задача 13213. Один студент выучил 20 из 25 вопросов программы, а второй – только 15. Каждому задают по одному вопросу. Найти вероятность того, что правильно ответят: а) оба студента, б) только один из них, в) только первый студент, г) хотя бы один из студентов.

Задача 13214. Океанологический зонд состоит из четырех независимо работающих узлов: U - узла питания, V и W- приборных узлов, I - узла передачи информации. Узлы V, W и I - каждый – состоят из независимо работающих блоков: V - из двух, W - из трех, I - из двух, если отказывает хотя бы один из блоков, то отказывает и весь узел. Надежность работы (то есть вероятность безотказной работы) в течение времени Т: узла U равна 0,6, каждого блока узла V - 0,7; каждого блока узла W - 0,8; каждого блока узла I - 0,75. Зонд отказывает в работе в случае выхода из строя или обоих приборных узлов, или узла питания, или узла передачи информации. Найдите вероятность того, что по истечении времени Т зонд все еще будет работать.

Задача 13215. В партии m изделий (m > 50). Вероятность брака изделия равна 0,05. Сколько нужно взять изделий из этой партии, чтобы с вероятностью, не меньшей, чем 0,9, среди них было хотя бы одно бракованное?

Задача 13216. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,9. Найти вероятность того, что: 1) только один из стрелков поразит цель; 2) только два стрелка поразят цель; 3) все три стрелка поразят цель.

Задача 13217. Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,7, при втором – 0,8, а при третьем – 0,9. Определить вероятность, что будет только одно попадание.

Задача 13219. На компьютере проводится эксперимент, в результате которого на дисплее появляется одно и только одно из первых натуральных чисел (1, 2, 3, …, 2n). Вероятность появления числа k равна 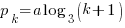, где a=const. Найдите:
А) величину a,
Б) вероятность того, что появилось число 2, если известно, что в результате опыта появилось четное число.
Вычислите a и эту вероятность при n=4.

Задача 13220. Симметричная игральная кость подбрасывается n раз. Какова вероятность того, что хотя бы раз выпадет шесть очков? Как себя ведет эта вероятность при бесконечно больших значениях n?

Задача 13221. В цехе работают 3 станка. Вероятность отказа в течение смены для станков соответственно равна 0,1, 0,2 и 0,15. Найти вероятность того, что в течение смены безотказно проработают два станка.

Задача 13222. Четыре орудия залпом выстрелили по цели. Вероятности попадания в цель при одном выстреле каждого орудия соответственно равны: 0,9; 0,8; 0,7 и 0,6. Найдите вероятность того, что в цель попало точно одно орудие.

Задача 13223. По оценкам экспертов, хотя бы один из проектов А и В принесет прибыль с вероятностью 0,7, оба же проекта будут прибыльными с вероятностью 0,4. В случае, если проект А окажется прибыльным, проект В также обеспечит прибыль с вероятностью 0,5. Какова вероятность прибыльности для каждого из проектов в отдельности?

Задача 13224. Стрелок попадает в цель с вероятностью, равной 0,6. Найти вероятность того, что для поражения цели ему понадобится выстрелить не более трех раз.

Задача 13225. Двое стрелков ведут стрельбу по мишени. Вероятность поражения цели первым стрелком - 0.8, вторым - 0.9. Каждый производит по три выстрела. Найти вероятность того что мишень будет поражена одной пулей.

Задача 13228. В одной урне 5 белых и 4 черных шара, во второй – 3 белых и 2 черных шара. Из каждой урны вынимают по 2 шара. Найти вероятность того, что среди 4 вынутых шаров только два белых.

Задача 13229. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,9, для второго – 0,8, для третьего – 0,7. Вычислите вероятность того, что по крайней мере один из станков не потребует внимания рабочего в течение часа.

Задача 13230. Два стрелка стреляют по одному зайцу. Вероятность попадания у первого стрелка 0,31, а у второго 0,4. Какова вероятность, что в зайца попадут? Какова вероятность, что в зайце будет 2 дырки?

Задача 13231. В мешке 5 белых, 4 черных и 3 синих шара. Три раза вытаскивают шар и кладут его обратно. Какова вероятность последовательности: белый, черный, синий?

Задача 13232. В мешке 5 белых, 4 черных и 3 синих шара. Три раза вытаскивают шар и не кладут его обратно. Какова вероятность последовательности: белый, черный, синий?

Задача 13233. В мешке имеются 3 красных и 4 белых шара. Три раза извлекается шар и сразу кладется обратно. Какова вероятность того, что все они будут красными?

Задача 13235. В двух коробках находятся электролампы одинаковой величины и формы, но разной мощности. В первой коробке 4 лампы на 60 ватт и 6 на 100 ватт; во второй соответственно – 5 и 7. Из обеих коробок наудачу берут по одной лампе. Какова вероятность того, что обе лампы одинаковой мощности?

Задача 13236. Три спортсмена участвуют в отборочных соревнованиях. Вероятности зачисления в сборную команду первого, второго и третьего спортсменов соответственно равны 0,8; 0,7; 0,5. Найти вероятность того, что хотя бы один из этих спортсменов попадет в сборную.

Задача 13237. Вероятность ошибки при составлении бухгалтерского баланса равна 0,3. Вероятность того, что аудитор пропустит ошибку, при проверке баланса равна 0,05. Найти вероятность того, что: а) ошибку допустит и бухгалтер и аудитор; б) ошибется хотя бы один из них; в) ошибок не будет.

Задача 13238. Вероятность попадания в цель при стрельбе из трех орудий таковы: р1=0,75; р2=0,80; р3=0,85. Какова вероятность того, что в мишень попадет только второй стрелок?

Задача 13239. Три стрелка стреляют по одной мишени, делая независимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,7, для второго 0,8, для третьего 0,6. Найти вероятность того, что попадет в мишень хотя бы один стрелок.

Задача 13240. Есть три урны. В первой находится 6 черных и 3 белых шара, во второй – 5 черных и 7 белых шаров, в третьей – 4 черных и 8 белых шаров. Из каждой урны вынимают по одному шару. Найти вероятность того, что все эти шары одного цвета.

Задача 13241. В некотором обществе 5% «левшей». Каков должен быть объем случайной выборки (с возвращением), чтобы вероятность встретить в ней хотя бы одного «левшу» была не менее 0, 95?

Задача 13242. Три стрелка, вероятности попадания в цель у которых равны 0,8; 0,7; 0,9 соответственно, делают по одному выстрелу в одну и ту же мишень. Найти вероятность того, что мишени будут две пробоины?

Задача 13243. В одной урне находится 4 белых и 8 черных шаров, а в другой 3 белых и 9 черных. Из каждой урны вынули по шару. Какова вероятность того, что оба шара окажутся белыми?

Задача 13244. Вероятность того, что студент успешно напишет контрольную работу по математике, равна 0,6, по физике – 0,5, по информатике – 0,8. Найти вероятность того, что студент не справится с контрольной работой только по одному предмету.

Задача 13245. Вероятности сдать зачет по информатике, экзамены по языку и философии соответственно равны 0,9; 0,7; 0,8. Найти вероятности того, что студент:
А) получил зачет, но не сдал ни одного экзамена,
Б) сдал только один экзамен,
В) не сдал ничего,
Г) сдал все.

Задача 13246. Прибор состоит из трех элементов K1, K2 и K3, вероятности отказа которых соответственно равны 0,1; 0,2; 0,2. Прибор выходит из строя при отказе элемента K1 или одновременном отказе элементов K2 и K3. Найти вероятность того, что прибор не выйдет из строя.

< Предыдущая 1 ... 21 22 23 24 25 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.