Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.
События. Теоремы сложения и умножения: список решений задач
Ниже даны ссылки на страницы с текстами задач на тему "События. Теоремы сложения и умножения". Все задачи имеют полное и качественное решение.
События. Теоремы сложения и умножения: теория и задачи
В некоторых задачах теории вероятности искомые события можно выразить через другие, более простые (сложное событие через элементарные), используя сумму и произведение событий (см. ниже определение). Тогда для вычисления вероятности такого сложного события используют соответствующие теоремы сложения и умножения вероятностей.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теперь приведем теоремы умножения и сложения вероятностей, которые описывают правила вычисления вероятностей сложных событий.
Теорема о сложении вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий А и В равна сумме вероятностей этих событий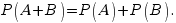 
Эта формула действует для любого числа попарно несовместных событий:
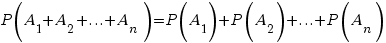
Также из этой формулы можно получить простое следствие о вероятности противоположного события: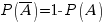 
, так как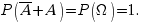 
Теорема о сложении вероятностей совместных событий. Вероятность суммы совместных событий вычисляется по формуле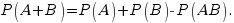 
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей независимых событий. Вероятность произведения независимых событий А и В равна произведению вероятностей этих событий: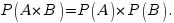 
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности: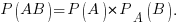 
Здесь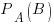 
- условная вероятность события В, при условии, что событие А произошло.
Формула для вычисления условной вероятности: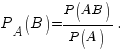 
Наступление хотя бы одного события. Вероятность появления хотя бы одного из независимых в совокупности событий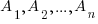 
равна разности между единицей и произведением вероятностей противоположных событий 
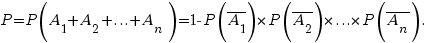Если указанные события имеют одинаковую вероятность p, то формула принимает вид: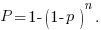 
Пример. Два стрелка стреляют в цель по одному разу каждый. Вероятность попадания в цель для первого стрелка равна 0,8, для второго – 0,9. Найти вероятность, что будет: а) два попадания; б) хотя бы одно попадание; в) ровно одно попадание.
Решение. Введем независимые события
А – попадание первого стрелка,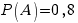 
;
В – попадание второго стрелка,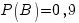 
.
Противоположные события: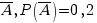 
- промах первого стрелка, 
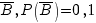- промах второго стрелка.
Найдем нужные вероятности.
а) Ровно два попадания. Это событие АВ, по теореме умножения вероятностей получаем: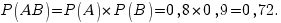 
б) Хотя бы одно попадание. Это событие А+В, его вероятность: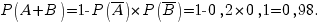 
в) Ровно одно попадание, событие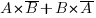 
, его вероятность:
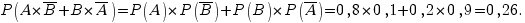
Пример. В первом ящике находится 2 белых и 5 черных шаров, во втором ящике - 3 белых и 2 черных шара. Из каждого ящика вынимают по одному шару. Найти вероятность того, что оба вынутых шара - черные.
Решение. Введем независимые события: А – вынули черный шар из первого ящика,
B - вынули черный шар из второго ящика. Найдем вероятности событий по классическому определению вероятности (отношение числа черных шаров в ящике к общему числу шаров в этом ящике). Получаем:
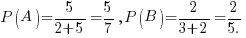
Тогда по теореме умножения вероятностей искомая вероятность есть:
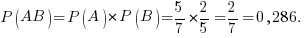
Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.