1 2 3 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3001 по 3051

Задача 3001. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

Задача 3002. Вероятность появления события А хотя бы один раз в трех независимых опытах равна 0,992. Какова вероятность появления события А в одном опыте, если в каждом опыте эта вероятность одинакова?

Задача 3003. Из таблицы случайных чисел наугад взято число. Рассмотрим 2 события: А - число делится на 5; В - число оканчивается нулём. Что означают события:
1) А*B
2) A+B
3) A * на событие, противоположное B
4) противоположное A * на противоположное B
5)противоположное А * на B

Задача 3004. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий:
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.

Задача 3005. Игра между А и В ведется на следующих условиях: первый ход всегда делает А, он может выиграть с вероятностью р1, если А не выигрывает, то ход делает В и может выиграть с вероятностью q1. Если В не выигрывает, то А делает второй ход, который может привести к его выигрышу с вероятностью р2 . Если А вторым ходом проигрывает, то победителем считается В. Найти вероятность выигрыша для первого и второго игроков.
р1=0.7, р2= 0.1, q1=0.9.

Задача 3006. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

Задача 3007. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Задача 3008. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными.

Задача 3009. Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0.05 и 0.08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

Задача 3010. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Задача 3011. В урне находятся 30 шаров, из них 15 белых, 8 черных и 7 красных. Определить вероятность извлечения красного или черного шара.

Задача 3012. Три электрических лампочки последовательно включены в цепь. Вероятность того, что одна (любая) лампочка перегорит, если напряжение в цепи превысит номинальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет.

Задача 3013. Два стрелка независимо друг от друга стреляют по одной и той же цели. Вероятность попадания для первого стрелка равна 0,8; для второго - 0,9. Найти вероятность поражения цели.

Задача 3014. В партии 10 деталей, из них 8 - стандартных. Найти вероятность того, что среди наудачу извлеченных двух деталей есть хотя бы одна стандартная.

Задача 3015. Найти вероятность того, что на 2 определенные карточки в «Спортлото «5 из 36» будет получено по минимальному выигрышу (угадано ровно три числа).

Задача 3016. Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2; 03, и 0,4. Какова вероятность получения одного попадания?

Задача 3017. Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на 1 и 2 вопросы равна 0,9 на 3 вопрос 0,8. найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на 2 вопроса.

Задача 3018. Стрелок стрелял в цель до первого промаха. Найти вероятность того, что у него после стрельбы останется хотя бы один патрон, если он получил 4 патрона и вероятность промаха при каждом выстреле равна 0,2.

Задача 3019. Вероятность попадания в мишень при 1-ом выстреле для 1-ого стрелка равна р, а для 2-го равна 0,7. Известно, что вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найти р.

Задача 3020. Стрелок стреляет по цели до 1-го попадания. Найти вероятность того, что у стрелка останется хотя бы один неизрасходованный патрон, если он получил 5 патронов и вероятность попадания в цель при каждом выстреле постоянна и равна 0,2.

Задача 3021. В жюри из 3 человек 2 члена независимо друг от друга принимают правильное решение с вероятностью 0.9, а третий для принятия решения бросает монету (окончательное решение выносится большинством голосов). С другой стороны, некий судья принимает решение с вероятностью 0.9. Кто с большей вероятностью принимает правильное решение: жюри или судья?

Задача 3022. По самолету производится 3 выстрела. Вероятность попадания при первом выстреле равна 0.5, при втором 0.6, третьем 0.8. При одном попадании самолет будет сбит с вероятностью 0.3, при двух с вероятностью 0.6,при трех – наверняка. Какова вероятность того, что самолет будет сбит?

Задача 3023. Для производственной практики на 30 студентов представлено 15 мест в Москве, 8 – в Самаре, 7 – в Саратове. Найти вероятность того, что два студента попадут на практику в один город.

Задача 3024. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить 4 бомбы, вероятности падения которых соответственно равны: 0.3, 0.4, 0.6, 0.7.

Задача 3025. Электрическая схема имеет вид:
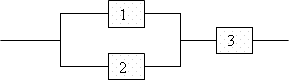
Вероятность выхода из строя блоков p1=0.1; p2=0.2; p3=0.6. Найти вероятность разрыва цепи.

Задача 3026. Первый стрелок имеет три патрона и стреляет до первого попадания. Оставшиеся патроны он передает второму стрелку. Какова вероятность, что второй попадёт хотя бы 1 раз, если вероятность попадания при одном выстреле для первого стрелка 0.8, а для второго 0.9?

Задача 3027. Найти вероятность прохождения тока через цепь, если вероятности исправной работы элементов указаны в схеме.
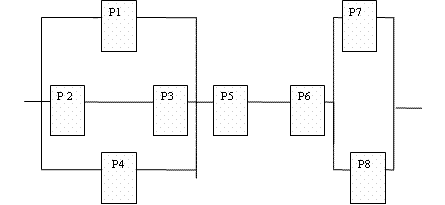
Элементы работают независимо друг от друга.

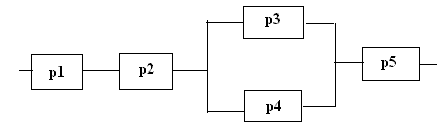
Задача 3028. Задана электрическая схема из 5 блоков. Надежность (вероятность безотказной работы) каждого блока равна соответственно p1=0.65, p2=0.75, p3=0.8, p4=0.85, p5=0.7. Считая выходы из строя различных блоков независимыми событиями, найти надежность всей схемы в целом.

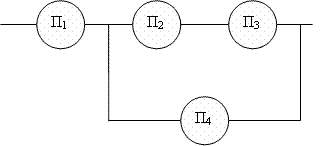
Задача 3029. Дана электрическая цепь, известны вероятности pi выхода из строя каждого прибора Пi, i=1,2,3,4. Найти вероятность того, что в цепи будет ток, если при выходе из строя прибор ток не пропускает. Принять p1=0.018, p2=0,440, p3=0,705, p4=0,830.

Задача 3030. Произведен залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0.85 , из второго - 0.91. Найти вероятность поражения цели.

Задача 3031. Вероятность попадания в цель только одним выстрелом из двух равна 0,32. Найти вероятность хотя бы одного попадания в цель при двух выстрелах.

Задача 3032. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа не потребует внимания первый станок, равна 0,9, второй – 0,8, третий – 0,85. Найти вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего.

Задача 3033. Три стрелка поочередно ведут стрельбу по одной и той же мишени. Каждый стрелок имеет два патрона. При первом же попадании стрельба прекращается. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,2, для второго – 0,3, для третьего – 0,4. Найти вероятность того, что все три стрелка израсходуют весь свой боезапас.

Задача 3034. Два стрелка стреляют по мишеням. Вероятность попадания при одном выстреле первым стрелком 0,018 , для второго 0,440. Найти вероятности того, что при двух залпах стрелки попадут только один раз, и что при двух залпах стрелки попадут хотя бы один раз.

Задача 3035. В колоде 36 карт. Наугад вынимают 4 карты. Найти вероятность того, что среди них окажется хотя бы один валет.

Задача 3036. Узел автомашины состоит из четырех деталей. Вероятности выхода этих деталей из строя соответственно равны: 0.04; 0.07; 0.05; 0.02. Узел выходит из строя, если выходит из строя хотя бы одна деталь. Найти вероятность того, что узел не выйдет из строя, если детали выходят из строя независимо друг от друга.

Задача 3037. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,6. Найти вероятность того, что при одном залпе в мишень попадет только один стрелок.

Задача 3038. При изготовлении детали заготовка должна пройти 4 операции. Предполагая появление брака на отдельных операциях событиями независимыми, найти вероятность изготовления стандартной детали, если вероятность появления брака на первой операции равна 0,03, на второй – 0,01, на третьей – 0,02, на четвертой – 0,05.

Задача 3039. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,98 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Задача 3040. В ящике среди 100 деталей находится одна бракованная. Из ящика наудачу извлечены 10 деталей. Найти вероятность того, что среди них окажется бракованная.

Задача 3042. Вероятности появления каждого из двух независимых событий А1 и А2 соответственно равны 0,7 и 0,6. Найти вероятность появления только одного из них.

Задача 3043. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Задача 3044. Вероятность хотя бы одного попадания в цель при трех выстрелах равна 0,875. Найти вероятность попадания в цель при одном выстреле.

Задача 3045. Для сигнализации о пожаре установлены два независимо работающих сигнализатора. Вероятность того, что при пожаре сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,80 для второго. Найти вероятность того, что при пожаре сработает только один сигнализатор.

Задача 3046. Ежедневно в течение 30 дней велся учет посетителей нотариальной конторы. Количество посетителей по дням приведены в соответствующих вариантах. Событие А заключается в том, что ежедневное количество посетителей является четным числом. Событие В заключается в том, что ежедневно количество посетителей заключено между числами 50 и 88 (включая эти числа). Определить:
1) Вероятность событий А и В, вероятность пересечения А и В, вероятность объединения А и В.
2) Зависит ли событие В от события А?
3) Зависит ли событие А от события В?
72 30 37 10 35 84 55 88 85 93 80 51 10 37
77 73 59 74 46 62 33 76 66 67 81 75 96 34 21 39

Задача 3047. Дано: P(A+B)=0,8, P(AB)=0,4, P(A|B)=0,6. Найти P(A), P(B), P(B|A) и выяснить, зависимы ли события A, B.

Задача 3048. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,3, второй – 0,6 третий – 0,4, и четвертый – 0,25. Найти вероятность того, что в течение смены
а) ни один станок не потребует внимания мастера,
б) хотя бы один потребует внимания мастера.

Задача 3049. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Задача 3050. Решить задачу, применяя теоремы сложения и умножения.
Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй - 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера; б) хотя бы один потребует внимания мастера.

Задача 3051. Решить задачу, применяя теоремы сложения и умножения. Бросают три игральных кости. Какова вероятность того, что на них выпадет по одинаковому числу очков?

1 2 3 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.