< Предыдущая 1 ... 3 4 5 6 7 ... 18 Следующая > 

Комбинаторика

Решения задач с 219 по 268

Задача 219. Решить уравнение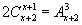

Задача 220. Сколькими способами можно составить маршрут путешествия, проходящего через 5 городов, если любой из маршрутов должен начинаться в одном из этих городов?

Задача 221. А) Сколько различных «слов», каждое из которых содержит 6 букв, можно составить из слова «экспертиза»?
Б) Сколько различных «слов», каждое из которых содержит 10 букв, можно составить из слова «экспертиза»?

Задача 222. В мореплаванье принято давать сигналы, используя разноцветные флаги. Сколько сигналов можно составить, используя одновременно 8 флагов, из которых 1 красный, 2 синих, 3 зеленых и 2 белых?

Задача 223. Имеется 20 наименований товаров. Сколькими способами их можно распределить по трем магазинам, если известно, что в первый магазин должно быть доставлено 8 наименований, во второй – 7 наименований, и в третьей – 5 наименований товаров?

Задача 224. Тридцать человек разбиты на три группы, по десять человек в каждой. Сколько может быть различных составов групп?

Задача 225. Комбинаторика. Сколькими способами можно разбить группу из 25 человек на две подгруппы по 10 и 15 человек?

Задача 226. Группа, состоящая из 27 человек, пишет контрольную работу из 3-х вариантов (каждый вариант по 9 человек). Сколькими способами можно выбрать 5 человек из группы так, чтобы среди них оказались писавшие все три варианта?

Задача 227. Сколькими способами можно поменять цифры в числе 143672 так, чтобы нечётные шли в порядке возрастания?

Задача 228. Комитет состоит из 20 человек. Минимальный кворум для принятия решения этим комитетом должен быть не менее 3/4 его состава. Определить, сколькими способами можно достичь минимального кворума.

Задача 229. В группе 28 студентов. Сколькими способами можно избрать 6 делегатов на профсоюзную конференцию?

Задача 230. В скольких точках пересекаются диагонали выпуклого 10-тиугольника, если никакие три из них не пересекаются в одной точке?

Задача 231. 28 костей домино распределены между 4 игроками поровну. Сколько возможно различных распределений?

Задача 232. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них оказалось не менее 2-х женщин. Сколькими способами это можно сделать?

Задача 233. В шахматном турнире участвуют 8 шахматистов третьего разряда, 6 – второго разряда и 2 – первого разряда. Определить количество таких составов одного тура, чтобы игроки одинаковой квалификации встречались только между собой.

Задача 234. Фирма планирует приобрести путевки для отдыха 25 сотрудников. Сколько существует вариантов приобретения путевок, если:
а) контракт будет заключен с четырьмя пансионатами?
б) с двумя пансионатами?

Задача 235. Автобусная компания обслуживает 10 маршрутов. Для обслуживания одного маршрута требуется 3 автобуса. В парке компании имеется 100 автобусов. Сколькими способами компания может выпустить автобусы на различные маршруты?

Задача 236. Сколько разных трехзначных чисел можно составить из цифр 1,2,3,4,5 при условии, что цифры могут повторяться?

Задача 237. В библиотеке на книжной полке расставлены 10 книг различных авторов, 8 студентов могут выбрать по одной книге. Сколько всевозможных вариантов выбора книг можно осуществить?

Задача 238. Шифр сейфа состоит только из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?

Задача 239. Фирма, имеющая 15 филиалов, решила подписаться на 15 различных периодических городских изданий. В городе печатается 30 видов периодической печати. Сколько существует способов подписки изданий при случайном выборе, если все издания будут поступать:
а) в главный офис,
в) в различные филиалы фирмы?

Задача 240. Числа 10, 11, 12,13,...,20 расставляются в один ряд. Сколько существует способов расстановки этих чисел таким образом, чтобы все четные числа стояли подряд?

Задача 241. В овощном магазине 3 сорта груш, два – апельсинов и 4 – яблок. Сколькими способами можно выбрать набор из трех различных фруктов, если взять по одному фрукту каждого вида?

Задача 242. Робот может выполнять движения «шаг вперед», «шаг назад», «шаг влево», «шаг вправо» и две операции: «взять предмет», «положить предмет». Сколько алгоритмов управления роботом можно составить, если он должен последовательно выполнить два различных движения и затем две различные операции?

Задача 243. Сколько подмножеств множества [10]={1,2,...,10} содержат по крайней мере одно нечетное число.

Задача 244. В учебной группе 36 студентов. Сколькими различными способами можно их разбить на бригады по 7 человек?

Задача 245. В рекламном агентстве имеется 13 агентов и четыре менеджера. Сколькими способами можно составить бригаду, состоящую из трех агентов и одного менеджера?

Задача 246. Сколькими способами можно составить сувенирный набор из трех различных предметов из 6 ложек, 6 вилок и 7 ножей?

Задача 247. В соревнованиях по рукопашному бою среди учебных заведений МВД России участвуют 20 спортсменов. Сколько боев будет проведено на этих соревнованиях?

Задача 248. Из колоды в 36 карт вынимают 8 карт. Указать число наборов, содержащих ровно 3 карты бубновой масти и 2 карты пиковой масти. Рассмотреть случаи выбора с возвращением и без возвращения. Производится упорядоченный выбор.

Задача 249. Во многих странах водительское удостоверение (автомобильные пра¬ва) имеют шифр, состоящий из трех букв и трех цифр. Чему равно общее число возможных номеров водительских удостоверений, считая, что число букв в латинском алфавите - 26, буквы занимают первые три позиции шифра если:
а) цифры и буквы в шифре не повторяются?
б) повторяются?

Задача 250. Рассматриваем буквы слова АТАМАН. Сколько имеется различных перестановок, в которых согласные идут в алфавитном порядке и буквы А не стоят?

Задача 251. Сколькими способами из колоды карт в 36 листов можно выбрать неупорядоченный набор из 5 карт так, чтобы в этом наборе были бы точно 1 валет, 2 дамы и 3 бубновых карты?

Задача 252. Сколько различных кодовых номеров можно составить из 9 десятичных цифр?

Задача 253. Выбрано 7 различных языков. Сколько потребуется словарей типа «Англо-русский и Русско-английский», чтобы можно было выполнять переводы между этими языками?

Задача 254. Сколькими способами из колоды карт в 36 листов можно выбрать упорядоченный набор из 6 карт для пасьянса так, чтобы в этом наборе были бы точно 2 короля, 2 дамы, 1 туз и 1 валет, причем 1 из королей и 1 дама были бы по краям?

Задача 255. Имеется 2 разные 3-х литровые банки и 6 разных литровых банок. Сколькими способами можно наполнить 6 литров воды, если выбранные банки должны быть наполнены?

Задача 256. Сколькими способами можно разложить 15 одинаковых мячей в 4 разные коробки?

Задача 257. Сколько можно образовать 4-х значных чисел из цифр 0, 1, 3, 4, 6, которые содержат хотя бы одну цифру 0?

Задача 258. Рассмотрим буквы фразы «ЗУБ ЗА ЗУБ». Сколько различных 3-х буквенных слов можно составить из букв этой фразы?

Задача 259. Сколькими способами 5 разных воробьев могут разместиться на 4 ветках, если на одной ветке может быть несколько воробьев?

Задача 260. Сколько существует способов раздать 10 различных марок 2 лицам по 5 штук?

Задача 261. Сколько различных кодовых номеров можно составить из 7 десятичных цифр?

Задача 262. Выбрано 6 различных языков. Сколько потребуется словарей типа «Англо-русский и Русско-английский», чтобы можно было выполнять переводы между этими языками?

Задача 263. Сколько пятизначных чисел можно составить из цифр 1, 2, 4, 6, 7, 8, если каждую цифру в любом числе использовать не более 1 раза? Сколько среди этих чисел будет чётных?

Задача 264. В чемпионате страны по футболу участвуют 18 команд. Каждые две команды встречаются на футбольных полях 2 раза. Сколько матчей играется в сезоне?

Задача 265. В филиале банка работает 15 сотрудников, трое из которых не имеют нужной квалификации. Сколько можно составить списков по 9 сотрудников, два из которых не имеют нужной квалификации?

Задача 266. Витя выписывает в порядке возрастания все числа, которые можно получить перестановкой цифр 1, 2, 3, 4, 5. Первым он выписал число 12345, последним – 54321. Какое число он выписал сразу после числа 42531? А перед ним? Сколько всего чисел он выписал?

Задача 267. Сколько различных четных трехзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5, если каждую цифру можно использовать только один раз?

Задача 268. Сколькими способами восемь монет различного достоинства можно разложить по двум карманам?

< Предыдущая 1 ... 3 4 5 6 7 ... 18 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.