Меню

Магазин задач » Задачи по теории вероятностей » Комбинаторика

инструкции по поиску решенных задач по теории вероятностей

Элементы комбинаторики: размещения, сочетания, перестановки. Решения задач

Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.




  Искать только в данном разделе

Комбинаторика: список решений задач

Ниже даны ссылки на страницы с текстами задач на тему "Комбинаторика". Все задачи имеют полное и качественное решение.

1 ... 7 8 9 10 11 ... 18 

Комбинаторика: теория и задачи

Рассмотрим некоторое множество Х, состоящее из n элементов 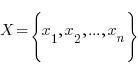X={lbrace}x_1, x_2, ..., x_n{rbrace}. Будем выбирать из этого множества различные упорядоченные подмножества Y из k элементов.

Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор 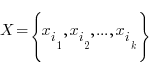X={lbrace}x_{i_1}, x_{i_2}, ..., x_{i_k}{rbrace} элементов множества Х.

Если выбор элементов множества Y из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле 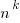n^k (размещения с повторениями).

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством
{A_{n}}^{k}=n(n-1)...(n-k+1)={n!}/{(n-k)!}
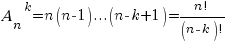
(размещения без повторений).

Пример. Пусть даны цифры: 7; 8; 9; 4; 5; 6. Определить сколько двузначных чисел можно составить из этих цифр.

Решение. Если цифры могут повторяться, то количество двузначных чисел будет 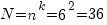N=n^k=6^2=36. Если цифры не повторяются, то N={A_6}^2=6*5=30.

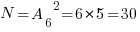Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно 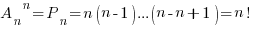{A_{n}}^{n}=P_n=n(n-1)...(n-n+1)={n!}.

Пример. На библиотечной полке стоят 30 книг, причем 27 - книги разных авторов и еще 3 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?

Решение. Временно объединим три книги одного автора в один объект, всего получим 28 объектов - 27 книг и 1 объект из трех книг. Для них число перестановок будет 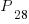P_28. Теперь три книги переставим между собой 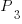P_3 способами. По правилу произведения получаем, что число способов расставить книги нужным образом равно: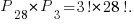 P_28*P_3=3!*28!.

Пусть теперь из множества Х выбирается неупорядоченное подмножество Y (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается 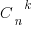{C_{n}}^{k} (от начальной буквы французского слова "combinasion", что значит "сочетание") и равно
{C_{n}}^{k}={{A_{n}}^{k}}/{k!}={n!}/{(n-k)!k!}.

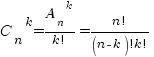Справедливы равенства:
{C_{n}}^{0}=1, {C_{n}}^{n}=1, {C_{n}}^{1}=n, {C_{n}}^{k}={C_{n}}^{n-k}.

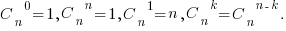
Пример. Учитель хочет назначить 3 студентов для уборки класс из учеников. Сколькими способами можно это сделать?

Решение. Так как порядок учеников не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27): 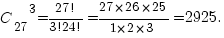{C_27}^3={27!}/{3!24!}={27*26*25}/{1*2*3}=2925.

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.