1 2 3 ... 13 Следующая > 

Геометрическая вероятность

Решения задач с 9001 по 9051

Задача 9001. Решить задачу, применяя непосредственный подсчет вероятностей по геометрическому определению вероятности.
В прямоугольник 5*4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?

Задача 9002. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?

Задача 9003. Обедая за столом, шириной 2 метра Вы увидели ползущего с другого конца стола на Ваш край таракана. Какова вероятность того, что, доползя до края стола, таракан проползет справа от Вас, если Вы сидите по центру стола и занимаете вдоль него 60 см, а таракан очень худой?

Задача 9004. В треугольник со сторонами, равными a, вписана окружность. Найти вероятность того, что точка, поставленная наудачу внутри треугольника, окажется в круге.

Задача 9005. Наудачу взяты два положительных числа х, y, каждое из которых не превышает 7/. Найти вероятность р того, что их произведение х*у будет не более 5 ,а частное у/х не больше 10/7.

Задача 9006. Решить задачу, применяя непосредственный подсчет вероятностей по геометрическому определению вероятности.
Прямоугольник 3*6 см2 разделен диагоналями на 4 части. Какова вероятность того, что наудачу поставленная в прямоугольник точка окажется в одном из треугольников с большим основанием.

Задача 9007. Решить задачу, применяя непосредственный подсчет вероятностей по геометрическому определению вероятности.
В круг радиуса R помещен маленький круг радиуса r. Найти вероятность того, что точка, наудачу поставленная в большой круг, попадет и в малый круг.

Задача 9008. Решить задачу, применяя непосредственный подсчет вероятностей по геометрическому определению вероятности.
В равносторонний треугольник, со стороной a вписана окружность. Найти вероятность того, что точка случайно поставленная в треугольник, окажется в пределах круга.

Задача 9009. На интервале (0,1) наудачу берутся 2 точки x и y. Какова вероятность того, что выполняется следующее условие:

Задача 9010. Действительная и мнимая части комплексного числа z произвольным образом выбираются из отрезка [0;2]. Найти вероятность того, что .

Задача 9011. Найти вероятность, что сумма наудачу взятых положительных правильных дробей не больше 0.95, а произведение не меньше 3/20.

Задача 9012. На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС будет меньше расстояния от точки О до ближайшей к ней точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Задача 9013. Шар X² +Y² +Z² =9 помещен внутри эллипсоида (X²/25)+(Y²/16)+(Z²/9)=1. Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.

Задача 9014. Два студента условились встретиться в определенном месте между 13 и 15 часами дня. Пришедший первым ждет второго в течение 1 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 13 до 15 часов).

Задача 9015. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равно возможно в любой момент промежутка времени длительности T. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если промежуток времени между моментами поступления сигналов меньше t, t<T. Найти вероятность того, что сигнализатор срабатывает за время T, если каждое из устройств пошлет по одному сигналу.

Задача 9016. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше 1, не превзойдет единицы, а их произведение будет не больше 0,25.

Задача 9017. Наудачу взяты 2 положительных числа x и y, каждой из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше 13/4, а частное x/y не больше 7/4.

Задача 9018. Решить задачу, применяя непосредственный подсчет вероятностей по геометрическому определению вероятности.
В круг радиуса 3 см вписан правильный треугольник. Найти вероятность того, что точка, поставленная наугад в круг, окажется в треугольнике.

Задача 9019. Из прямоугольника (0,0), (0,2), (?,2), (?,0) случайным образом выбрана точка. Какова вероятность того, что точка принадлежит области, заключенной между y=sin(x) и y=sin(2x).

Задача 9020. Шкала секундомера имеет цену деления 2 сек. Какова вероятность сделать отсчет с ошибкой не более 0,5 сек., если отсчет округляется до целого деления в ближайшую сторону.

Задача 9021. Спутник Земли движется по орбите, которая заключена между 60^o северной и 60^o южной широты. Считая падение спутника в любую точку поверхности Земли между указанными параллелями равновозможным, найти вероятность того, что спутник упадет выше 30^o северной широты.

Задача 9022. На отрезке MC длиной 10 см наудачу поставлены две точки A и B. Найти вероятность того, что точка A будет ближе к точке B, чем к точке M.

Задача 9023. В круг вписан квадрат. Найти вероятность того, что случайная точка, брошенная в круг, не попадет в квадрат.

Задача 9024. Найти , где x,y любые числа из [6;8].

Задача 9025. Найти , где x,y любые числа из [1;3].

Задача 9026. Найти , где x,y любые числа из [2;4].

Задача 9027. Найти , где x,y любые числа из [0.5;2].

Задача 9028. В круг радиуса r бросают 7 точек. Найти вероятность того, что 3 из них попадут в квадрат, вписанный в этот круг.

Задача 9029. Найти , где x,y любые числа из [0;4].

Задача 9030. На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОB и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Задача 9031. В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину 1/k. k=5.

Задача 9032. Моменты начала двух событий наудачу распределены в промежутке времени от T1 до T2. Одно из событий длится 10 мин., другое – t мин. Определить вероятность того, что: а) события «перекрываются» по времени; б) «не перекрываются». T1=1000; T2=1200; t=20.

Задача 9033. Какова вероятность того, что из трех взятых наудачу отрезков длины не более l можно построить треугольник?

Задача 9034. Телефонная линия, соединяющая два пункта А и В, расстояние между которыми равно 7 км, оборвалась в неизвестном месте. Какова вероятность того, что место обрыва удалено от обоих пунктов далее чем на 2,5 км.

Задача 9036. Радиус круга 4 см. Найти вероятность того, что наудачу поставленная в круг точка окажется внутри вписанного квадрата.

Задача 9037. Внутри круга радиусом 20 см проведены 2 непересекающиеся окружности – одна радиусом 5 см, другая – 10 см. Найти вероятность того, что точка, взятая наудачу внутри большего круга, окажется лежащей внутри одного из малых кругов?

Задача 9038. Найти вероятность того, что точка, поставленная в круг радиуса R, окажется в заштрихованной части.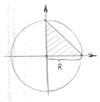

Задача 9039. В круг случайным образом брошена точка так, что её любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри вписанного в круг другого круга, радиус которого вдвое меньше.

Задача 9040. Действительная и мнимая части комплексного числа z произвольным образом выбираются из отрезка [0;2]. Найти вероятность того, что Im (1/z)+1/4<0.

Задача 9041. В течение 10 единиц времени в устройство должны поступить два сообщения: одно длительностью a=4 единиц, другое – b=3 единиц. Устройство не может принимать второе сообщение, если не закончилось первое. Какова вероятность того, что будет принято только одно сообщение?

Задача 9042. Точка с координатой x выбирается наудачу на отрезке [-1;1], и независимо от нее точка с координатой y выбирается наудачу на отрезке [0;2]. Проверить, являются ли три события {x+y<1}, {x>0} и {y<<1} независимыми в совокупности.

Задача 9043. Точка с координатой x наудачу выбрана на отрезке [1;3] и независимо от нее точка с координатой y наудачу выбрана на отрезке [0;2]. Найти вероятность события {2x+y>3}.

Задача 9044. На отрезок [-1;1] наудачу и независимо друг от друга брошены две точки с координатами x и y.
А) проверить, являются ли события {y>0} и {min(x,y)≤0} независимыми.
Б) проверить, являются ли события {x<0}, {x>1/2} и {x=0} независимыми в совокупности.

Задача 9045. На плоскости начерчены две концентрические окружности, радиусы которых 5 см и 10 см. На большую окружность наудачу брошена точка. Найти вероятность попадания точки в кольцо, образованное этими окружностями.

Задача 9046. Внутрь круга радиусом 4 см наудачу брошен дротик. Найти вероятность того, что он попадет в правильный треугольник, вписанный в данный круг.

Задача 9047. В квадрат со стороной 4 см вписаны 4 соприкасающихся круга с радиусом 1 см. Найти вероятность того, что наудачу брошенная точка не попадет ни в один круг.

Задача 9048. Внутрь круга радиусом 2 см наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата.

Задача 9049. Поезда данного маршрута городского трамвая идет с интервалом в 5 минут. Пассажир подходит к остановке в некоторый момент времени. Считая момент прихода пассажира распределенным равномерно, найти вероятность появления пассажира не ранее чем через минуту после ухода предыдущего поезда, но не позднее, чем за две минуты до отхода следующего поезда.

Задача 9050. Найти вероятность того, что функция z=5x+2y примет значение меньше четырех, если аргументы x и y выбираются наудачу из промежутка (0;1).

Задача 9051. На отрезке L длины 35 см помещен меньший отрезок l длины 20 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок.

1 2 3 ... 13 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.