< Предыдущая 1 ... 15 16 17 18 19 ... 47 Следующая > 

Дискретная случайная величина

Решения задач с 6807 по 6856

Задача 6807. В хлебопекарне выпекают булочки с изюмом. Какое наименьшее количество изюма нужно положить в тесто, из которого будет 800 булочек, чтобы вероятность найти в произвольно взятой булочке по крайней мере две изюминки была равна примерно 0,995?

Задача 6808. В среднем на лекции по математике отсутствует 10 человек. Считая, что число пропусков подчинено закону Пуассона, найти вероятность того, что отсутствовать будет целая группа (20 человек).

Задача 6809. На телефонной станции в течение одного часа возникает в среднем 60 вызовов. Какова вероятность того, что в течение одной минуты возникает ровно 2 вызова.

Задача 6810. По цели, вероятность попадания в которую равна 0,3, сброшено одиночно 4 бомбы. Построить многоугольник и функцию распределения числа попаданий в цель. Найти моду, математическое ожидание, среднее квадратическое отклонение.

Задача 6811. Среднее число импульсов в секунду хаотической импульсной помехи, подчиняющейся закону распределения вероятностей Пуассона, равна 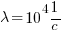. Найти вероятность попадания двух импульсов в интервал τ=100 мкс.

Задача 6812. В партии из 10 деталей имеется одна бракованная. Чтобы ее обнаружить, выбирают в случайном порядке одну деталь за другой и каждую проверяют. Пусть Х – число проверенных деталей, включая бракованную. Найти закон распределения, математическое ожидание и дисперсию дискретной случайной величины Х.

Задача 6813. Из сосуда, содержащего 3 белых и 2 чёрных шара, вынимают 3 шара и перекладывают в другой сосуд, где находятся 1 белый и 2 чёрных шара. Для случайного числа белых шаров во втором сосуде найти:
а) закон распределения и построить многоугольник распределения;
б) математическое ожидание;
в) дисперсию и среднее квадратическое отклонение
г)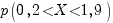

Задача 6814. Студент в сессию должен сдать 3 экзамена, причем известно, что положительную оценку он может получить на них с вероятностями 0,4, 0,9, 0,3. Предполагая, что различные экзамены представляют собой независимые испытания, построить ряд распределения и многоугольник распределения случайной величины X - числа успешно сданных экзаменов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение X. Найти вероятности того, что студент: а) не сдаст ни одного экзамена, б) студент сдаст ровно два экзамена, в) студент сдаст хотя бы один экзамен.

Задача 6815. Шестигранный кубик бросили четыре раза. Пусть ξ - случайная величина, равная количеству выпавших пятерок или двоек. Найти функцию распределения ξ, Mξ, Dξ.

Задача 6816. Вероятность того, что аудитор допустит ошибку при проверке одного предприятия, равна 0,4. Аудитор проверяет пять предприятий. Пусть ξ - случайная величина, равная количеству ошибок аудитора. Найти функцию распределения ξ, Mξ, Dξ.

Задача 6817. Отчеты показали, что 50% посетителей банка приходят в него для уплаты коммунальных платежей. Составить ряд распределения и найти числовые характеристики числа посетителей, пришедших внести платежи, среди 6 человек, находящихся сейчас в очереди. Найти вероятность того, что как минимум пять из них пришли сюда по какой-либо другой причине.

Задача 6818. Из партии, состоящей из 100 изделий, среди которых имеется 10 бракованных, выбраны случайным образом 5 изделий для проверки их качества. Построить ряд распределения случайного числа Х бракованных изделий, содержащихся в выборке.

Задача 6819. В лотерее 1000 билетов. Из них на один билет выпадает выигрыш 50 руб, на 10 билетов – выигрыш по 10 руб, на 50 билетов – по 2 руб, остальные невыигрышные. Куплен один билет. Найти вероятность выиграть не менее 2 руб.

Задача 6820. Двое поочередно бросают монету до первого появления герба. Игрок, у которого выпал герб, получает от другого игрока 1 рубль. Найти математическое ожидание выигрыша каждого игрока.

Задача 6821. Запишите таблицу для данного закона распределения случайной величины X, постройте многоугольник распределения. Найдите числовые характеристики распределения. Запишите функцию распределения и постройте ее график. Ответьте на вопрос о вероятности описанного события.
Записи страховой компании показали, что 30% держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. Для проверки в случайном порядке было отобрано пять человек старше 50 лет, имеющих полисы. Случайная величина X — количество потребующих возмещения среди отобранных. Чему равна вероятность того, что потребуют возмещения более трех человек?

Задача 6822. Рабочий обслуживает 6 однотипных станков, расположенных в ряд с равными интервалами. Закончив обслуживание какого-либо станка, рабочий переходит к тому станку, который раньше других потребовал внимания (остановка, авария и т.п.). Найти ряд, ф.р. и м.о. (среднее значение) длины перехода рабочего, если станки выходят из строя с равными вероятностями.

Задача 6823. Запишите таблицу для данного закона распределения случайной величины X, постройте многоугольник распределения. Найдите числовые характеристики распределения. Запишите функцию распределения и постройте ее график. Ответьте на вопрос о вероятности описанного события.
В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает пять счетов. Вероятность наличия ошибки в каждом счете — величина постоянная и равна 0.03. Случайная величина X — количество счетов с ошибкой. Какова вероятность того, что хотя бы один счет будет ошибкой?

Задача 6824. Решите задачу, используя формулы биномиального распределения:
Вероятность того, что посаженное дерево приживется, равна 0,9. Найдите закон распределения случайной величины Х – числа прижившихся деревьев среди трех посаженных. Вычислите математическое ожидание и дисперсию случайной величины Х.

Задача 6825. В мастерскую по ремонту бытовой техники поступили 8 холодильников, из которых 3 подлежали гарантийному обслуживанию. Бригада специалистов, работающая в первую смену, получила наряд на ремонт 4 холодильников.
а) Составьте ряд распределения числа холодильников, отремонтированных по гарантии в первую смену; если холодильники для ремонта отбирались случайным образом и постройте его график;
б) Найдите числовые характеристики этого распределения;
в) Запишите функцию распределения вероятностей и постройте ее график;
г) Определите вероятность того, что по гарантии было отремонтировано не более двух холодильников.

Задача 6826. Среднее число ошибочных соединений, приходящееся на одного телефонного абонента в единицу времени, равно 8. Какова вероятность того, что для данного абонента число ошибочных соединений будет больше 4?

Задача 6827. Фирма имеет 4 грузовых автомобиля. Вероятность выхода на линию каждого автомобиля равна 0,8. Составить закон распределения случайной величины Х – числа автомобилей, которые выйдут на линию в произвольно выбранный день. Найти математическое ожидание и дисперсию этой случайной величины.

Задача 6828. Вероятность превысить заданную точность при измерении равна 0,4. Составить закон распределения случайной величины Х – число ошибок при 10 измерениях. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

Задача 6829. В 1 ящике – 2 белых и 3 черных шара, во 2 ящике – 3 белых и 3 черных шара. Из каждого ящика вынимают по одному без возврата 2 шара. Случайная величина Х – число вынутых белых шаров. Найти M(X) и D(X).

Задача 6830. Производится три последовательных опыта, в каждом из которых событие А появляется с вероятностью 0,6. Построить ряд распределения и функцию распределения числа появлений события А в 3-х опытах. Найти m_X, D_X (2 способа).

Задача 6831. Рассматривается работа трех независимо работающих технических устройств (ТУ). Вероятность нормальной работы первого ТУ равна 0,2; второго - 0,4; третьего - 0,5. Построить закон распределения числа работающих ТУ. Найти М(х), D(x), σ(x).

Задача 6832. В первой коробке лежат три хороших и две бракованных детали, во второй – четыре хороших и одна бракованная, а в третьей – две хорошие и три бракованные детали. Для контроля из каждой коробки наугад берут по одной детали. Составить закон распределения числа бракованных деталей среди отобранных, написать функцию распределения этой случайной величины и построить ее график.

Задача 6833. В некотором цехе брак составляет 5% всех изделий. Х - число бракованных изделий из трех взятых на проверку. Для этой случайной величины
а) построить ряд распределения, многоугольник распределения, функцию распределения;
б) найти математическое ожидание, среднее квадратичное отклонение;
в) вероятность того, что среди этих трех изделий будет не менее двух бракованных.

Задача 6834. Производятся последовательные независимые испытания трех приборов на надежность. Надежность каждого из приборов равна 0,76. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Найти закон распределения случайной величины X - числа испытанных приборов, M(X), D(X), σ(X), P(1,5 ≤ X < 2,9).

Задача 6835. Производится три независимых выстрела в мишень. Вероятность попадания при каждом выстреле равна 0,2. Пусть Х – число попаданий в мишень.
1) составить закон распределения случайной величины Х.
2) вычислить числовые характеристики случайной величины Х.
3) записать функцию распределения случайной величины.
4) Вычислить P(X > m_X).

Задача 6836. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х. Построить график функции распределения и найти вероятность события X ≤ 3 при следующих условиях. У стрелка, вероятность попадания которого в мишень равна 0,65 при каждом выстреле, имеется 5 патронов. Стрельба прекращается при первом же попадании. X - число оставшихся патронов.

Задача 6837. Математическое ожидание годового количества осадков для данной местности равно 600 мм. Каково минимальное количество осадков за год с вероятностью, не превышающей величины 0,8?

Задача 6838. На контроль качества поступила партия из n = 6 деталей. Вероятность того, что деталь окажется бракованной, равна 0,15.
а) найти вероятности P_n(k) того, что число бракованных деталей k в партии составляет 0, 1, …, 6;
б) построить ломаную линию с вершинами в точках (k, P_n(k));
в) найти наивероятнейшее число бракованных деталей двумя способами: непосредственно по определению и по формуле.

Задача 6839. Среди 11 изделий 6 изделий первого сорта. Наудачу выбрали 3 изделия. Случайная величина X – число первосортных изделий среди выбранных трех изделий.
1. Составить закон распределения случайной величины X.
2. Построить полигон относительных частот.
3. Найти функцию распределения F(x) случайной величины X, построить ее график.
4. Найти характеристики случайной величины X:
а) математическое ожидание M(X);
б) дисперсию D(X), среднее квадратическое отклонение σ(Х);
в) моду Mo.

Задача 6840. Скорость ветра в сутки является случайной величиной, математическое ожидание которой равно 55,20 м/ч. Оценить вероятность того, что скорость ветра за следующие сутки будет от 38,40 до 72,00 м/ч. Известно, что среднее квадратическое отклонение скорости ветра равно 9,900.

Задача 6841. Бомбардировщик сбрасывает бомбы на цель до первого попадания, но успевает сбросить не более четырех бомб. Вероятность попадания при одном сбрасывании равна 0,9. Составить закон распределения числа сброшенных бомб.

Задача 6842. Средняя длина изготовленных заводами металлических стержней равна 68,4 м. Оценить вероятность того, что наугад выбранный стержень будет иметь длину от 52,8 до 84 м. Известно, что среднее квадратическое отклонение длины стержней равно 12,1.

Задача 6843. В 5 килограммах находится в среднем 3 пораженных семени. Найти вероятность, что в 3,33 килограммах поражено: А) ровно 4, Б) не более 4 семян.

Задача 6844. Вероятность, что студент получит на экзамене отличную оценку, равна 0,7. Составить закон распределения числа отличных оценок, если студент сдавал 4 экзамена.

Задача 6845. Автозавод производит автомашины, каждая из которых доброкачественная с вероятностью 0,7. Покупатель при покупке одной автомашины имеет право испробовать не более четырех. Составить закон распределения числа опробованных покупателем автомашин, если проверка идет до первой доброкачественной.

Задача 6846. Производятся последовательные независимые испытания пяти приборов на надёжность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надёжным. Требуется:
А) найти закон распределения для случайного числа Х испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9;
Б) построить многоугольник распределения;
В) найти вероятность события X < 3;
Г) найти математическое ожидание и дисперсию случайной величины Х.

Задача 6847. Игральную кость бросают 5 раз. Составить закон распределения случайной величины Х – число выпавших очков кратно трем. Найти M(X) и D(X).

Задача 6848. Среднее число вызовов, поступающих на АТС в минуту равно 120. Найти вероятности следующих событий:
А=(за 2 секунды на АТС не поступит ни одного вызова),
В = (за 2 секунды на АТС поступит менее двух вызовов),
С = (за 1 секунду на АТС поступит хотя бы один вызов.)

Задача 6849. В среднем в магазин заходят 3 человека в минуту. Найти вероятность того, что за 2 минуты в магазин зайдет не более 1 человека.

Задача 6850. В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Найти закон распределения, основные числовые характеристики и функцию распределения числа стандартных деталей среди отобранных.

Задача 6851. Вероятность того, что деталь прошла проверку ОТК равна 0,8. Оцените с помощью неравенства Чебышева вероятность того, что среди 400 случайно отобранных деталей окажутся непроверенными от 60 до 100 деталей. Уточнить результат с помощью интегральной теоремы Лапласа.

Задача 6852. В лотерее на 100 билетов разыгрываются две вещи, стоимость которых 150 и 50 рублей. Найти закон распределения и функцию распределения суммарного выигрыша для лица, имеющего один билет.

Задача 6853. Найти закон распределения указанной дискретной СВ и ее функцию распределения F(x). Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить график функции распределения F(x).
В первой коробке 10 сальников, из них 2 бракованных, во второй – 16 сальников, из них 4 бракованных, в третьей – 12, из них 3 бракованных. СВ – число бракованных сальников при условии, что из каждой коробки взято наугад по одному сальнику.

Задача 6854. Трех человек наугад останавливают на улице и спрашивают месяц их рождения. Составить закон распределения числа лиц, родившихся в один месяц. Построить ряд распределения, F(x), M(X), D(X), σ(X).

Задача 6855. Электронный экзаменатор задает 5 вопросов. Вероятность правильного ответа на любой из них равна 0,8. Составить закон распределения числа правильных ответов. Найти Mx, Dx, σ, P{X > 3}.

Задача 6856. В нашем распоряжении имеется 16 лампочек, каждая из них с вероятностью 0,75 без дефекта. Лампочку ввинчивают в патрон и подают напряжение, после чего дефектная лампочка сразу же перегорает и заменяется другой.
Рассматривается случайная величина Х – число лампочек, которое будет испробовано. Постройте ее ряд распределения и найдите математическое ожидание M(X).

< Предыдущая 1 ... 15 16 17 18 19 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.