www.matburo.ru МатБюро решение задач по теории вероятностей

История обновлений
Апрель 2023: 16900 задач
Ноябрь 2020: 14500 задач
Март 2019: 13600 задач
Ноябрь 2017: 11700 задач
Май 2017: 11400 задач
Октябрь 2016: 10600 задач
Октябрь 2015: 10300 задач
Август 2015: 10000 задач
Февраль 2015: 8600 задач
Апрель 2014: 8100 задач
Июль 2013: 7400 задач
Апрель 2013: 6800 задач
Январь 2013: 6500 задач

Магазин задач » Задачи по теории вероятностей » Дискретная случайная величина

Дискретная случайная величина, числовые характеристики, функция распределения. Решения задач

Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.

Дискретная случайная величина: список решений задач

Ниже даны ссылки на страницы с текстами задач на тему "Дискретная случайная величина". Все задачи имеют полное и качественное решение.

1 ... 22 23 24 25 26 ... 47

Дискретная случайная величина: теория и задачи

Дискретная случайная величина - это такая величина X, которая в каждом испытании принимает в точности одно, но случайное значение (которое нельзя предсказать заранее). Например, количество выпадений гербов при бросании двух монет - это дискретная случайная величина, которая может принимать значения 0, 1 и 2. Число значений может быть как конечным, так и сченым. Если каждому значению величины X вида 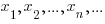x_1, x_2, ..., x_n, ... поставлена в соответствие вероятность 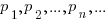p_1, p_2, ..., p_n, ... , то говорят, что задан закон распределения данной случайной величины X. Он может быть представлен в табличном виде (ряд распределения), аналитически (формулой) или графически (через функцию распределения).

Для исследования дискретной случайной величины часто в задачах требуется найти ее числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду. Приведем формулы для вычислений.

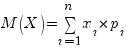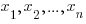Математическое ожидание дискретной случайной величины X можно найти по формуле: $M(X)=sum{i=1}{n}(x_i*p_i}$ , где x_1, x_2, ..., x_n - возможные значения случайной величины, а 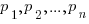p_1, p_2, ..., p_n - соответствующие им вероятности.

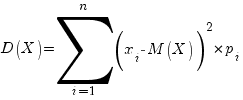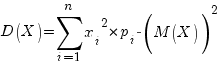Дисперсия дискретной случайной величины X определяется по формуле: $D(X)=sum{i=1}{n}((x_i-M(X))^2*p_i}$ или $D(X)=sum{i=1}{n}({x_i}^2*p_i}-(M(X))^2$ . В более компактной записи это: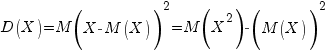 D(X)=M(X-M(X))^2=M(X^2)-(M(X))^2

Среднее квадратическое отклонение дискретной случайной величины X есть корень квадратный из дисперсии: 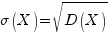sigma(X)=sqrt{D(X)} , оно характеризует меру разброса значений случайной величины относительно математического ожидания.

Мода дискретной случайной величины X - это наиболее вероятное ее значение, то есть такое значение 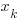x_k , что p_k=max(p_i) .

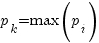Пример. На полке из 6 книг 3 книги по математике и 3 по физике. Выбирают наудачу три книги. Найти закон распределения числа книг по математике среди выбранных книг. Найти математическое ожидание этой случайной величины.

Решение. Введем дискретную случайную величину X = (Количество книг по математике среди 3 отобранных). X может принимать значения 0, 1, 2 и 3. Найдем соответствующие вероятности (по формуле гипергеометрической вероятности).
X=0, если все три книги – не по математике. Вероятность 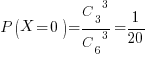$P(X=0)={{C_3}^3}/{{C_6}^3}=1/20$ .
X=1, если одна книга по математике и две – не по математике. Вероятность 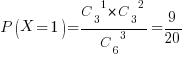$P(X=1)={{C_3}^1 * {C_3}^2}/{{C_6}^3}=9/20$ .
X=2, если две книги по математике и одна нет. Вероятность 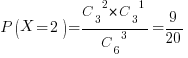$P(X=2)={{C_3}^2 * {C_3}^1}/{{C_6}^3}=9/20$ .
X=3, если все три книги – по математике. Вероятность 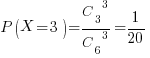$P(X=3)={{C_3}^3}/{{C_6}^3}=1/20$ .
Получаем закон распределения случайной величины X:
x_i 0 1 2 3
p_i 1/20 9/20 9/20 1/20
Математическое ожидание равно
$M(X)=sum{i=1}{4}(x_i*p_i} = 0*{1/20}+1*{9/20}+2*{9/20}+3*{1/20}={3/2}=1,5.$

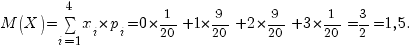
Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.