www.matburo.ru МатБюро решение задач по теории вероятностей

История обновлений
Апрель 2023: 16900 задач
Ноябрь 2020: 14500 задач
Март 2019: 13600 задач
Ноябрь 2017: 11700 задач
Май 2017: 11400 задач
Октябрь 2016: 10600 задач
Октябрь 2015: 10300 задач
Август 2015: 10000 задач
Февраль 2015: 8600 задач
Апрель 2014: 8100 задач
Июль 2013: 7400 задач
Апрель 2013: 6800 задач
Январь 2013: 6500 задач

Магазин задач » Задачи по теории вероятностей » Теоремы Лапласа

Приближенные формулы Лапласа (Муавра-Лапласа). Решения задач

Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.

Теоремы Лапласа: список решений задач

Ниже даны ссылки на страницы с текстами задач на тему "Теоремы Лапласа". Все задачи имеют полное и качественное решение.

1 ... 11 12 13 14 15 ... 25

Теоремы Лапласа: теория и задачи

Пусть мы находимся в условиях схемы Бернулли, то есть производится n независимых испытаний, в каждом из которых событие A может произойти с вероятностью p. В случаях, когда n достаточно большое для непосредственных вычислений и при этом произведение 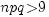npq>9 (вероятность не очень маленькая), можно применять приближенные формулы для вычисления вероятностей. Эти формулы носят название формул или теорем Лапласа, Муавра-Лапласа.

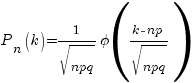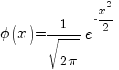Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то вероятность того, что событие A наступит в точности k раз, равна $P_n(k)=1/{sqrt{npq}} phi ({k-np}/{sqrt{npq}})$ , где $phi(x)=1/{sqrt{2pi}}e^{-{x^2}/2}$ - функция Гаусса (значения берутся из таблиц).

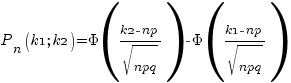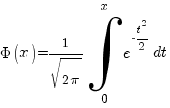Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то вероятность того, что событие A наступит от k1 до k2 раз, равна $P_n(k1; k2)=Phi ({k2-np}/{sqrt{npq}})-Phi ({k1-np}/{sqrt{npq}})$ , где $Phi(x)=1/{sqrt{2pi}} int{0}{x}{e^{-{t^2}/2} dt}$ - функция Лапласа (значения берутся из таблиц).

Для вычисления вероятности по формулам Лапласа полезно пользоваться свойствами данных функций:

1) phi({-x})=phi(x); Phi({-x})=-Phi(x)

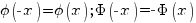
2) при больших 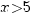x>5 верно phi(x)approx 0; Phi (x) approx 0,5 .

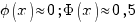Пример. На заводе изготавливается в среднем 75% деталей отличного качества. За час было изготовлено 400 деталей. Найти вероятность того, что среди них ровно 280 деталей отличного качества.

Решение. По условию 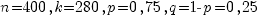n=400, k=280, p=0,75, q=1-p=0,25 . Подставляем в формулу Лапласа:
$P_{400}(280)=1/{sqrt{400*0,75*0,25}} phi ({280-400*0,75}/{sqrt{400*0,75*0,05}})=$ =0,115 phi (-2,31)= 0,115 phi (2,31)= 0,115*0,0277 approx 0,003.

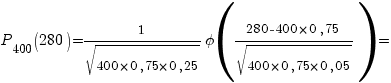
Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.