Меню

Магазин задач » Задачи по теории вероятностей » Формула Бернулли

инструкции по поиску решенных задач по теории вероятностей

Формула Бернулли: повторные независимые испытания. Решения задач

Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.




  Искать только в данном разделе

Формула Бернулли: список решений задач

Ниже даны ссылки на страницы с текстами задач на тему "Формула Бернулли". Все задачи имеют полное и качественное решение.

1 ... 22 23 24 25 26 ... 47 

Формула Бернулли: теория и задачи

При решении задач теории вероятности часто возникают ситуации, в которых одно и тоже испытание повторяется многократно, причем исход каждого испытания независим от исходов других и наступает с одинаковой вероятностью. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Пусть некоторое событие А наступает в каждом испытании с вероятностью 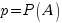p=P(A) (вероятность успеха). Обозначим за 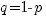q=1-p вероятность того, что событие А не наступит в испытании (вероятность противоположного события, неудачи). Произведем n независимых испытаний. Тогда вероятность 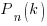P_n(k) того, что событие А в них наступило в точности k раз, можно найти по формуле Бернулли:
P_n(k)={C_n}^k*p^k*q^{n-k}={{n!}/{k!*(n-k)!}}*p^k*(1-p)^{n-k}

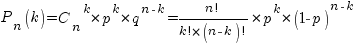
Вообще говоря, данную вероятность можно было вычислить непосредственно, используя теоремы сложения и умножения вероятностей. Но при достаточно большом количестве испытаний это трудоемкий путь. Формула Бернулли обобщает способ вычисления таких вероятностей и дает простой и удобный инструмент вычисления (Якоб Бернулли (1654 – 1705) – швейцарский математик).

Распределение числа успехов (появлений события А) носит название биномиального распределения.

Схема Бернулли позволяет установить, какое число появлений события А наиболее вероятно. Формула для наивероятнейшего числа появлений события А имеет вид: 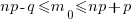np-q<=m_0<=np+p. При этом число 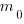m_0 может принимать либо одно значение 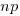np (когда 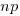np является целым числом), или два значения (когда целым является np-q).

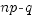Пример. Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах будет ровно 3 попадания в цель.

Решение. Подставляем в формулу Бернулли данные задачи n=5, k=3, p=0,7 и получаем:
P_5(3)={C_5}^3*0,7^3*0,3^{5-3}={{5!}/{3!*2!}}*0,7^3*0,3^2={{4*5}/{1*2}}*0,7^3*0,3^2=0,3087.

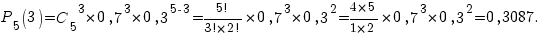
Пример. На склад из производственного цеха поступает в среднем 5% нестандартных деталей. Найти вероятность того, что среди взятых наудачу 10 деталей 2 будут нестандартными.

Решение. Событие А - «появление нестандартной детали», его вероятность 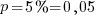p=5%=0,05, число деталей 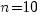n=10. По формуле Бернулли находим для k=2:
P_10(2)={C_10}^2*0,05^2*0,95^{8}={{10!}/{2!*8!}}*0,05^2*0,95^{8}={{9*10}/{1*2}}*0,05^2*0,95^{8}=0,075.

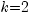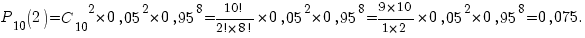
Другие примеры задач вы найдете на странице Примеры по теории вероятностей.