Проверка статистических гипотез
Решения задач с 3051 по 3066
Задача 3051. Исследовалась урожайность пшеницы на 80-ти сортоиспытательных участках, причем на 50 участках применялись одни условия выращивания, а на других 30 участках – другие. После сбора урожая выяснилось, что в первой группе число участников, имеющих урожайность не менее 22 ц с гектара, составляет 10, а во второй – 6. Можно ли считать доли таких участков одинаковыми, принять α равным 0,05.
Задача 3052. При обработке исторических материалов профессиональной переписи 1914 года были получены следующие данные: из 329 рабочих фабрики Тамбовской губернии на полевые работы уходило 146 человек, а из 494 рабочих фабрики Ярославской губернии уходило 263 человек. Проверить гипотезу о равенстве вероятности ухода рабочих на полевые работы для двух губерний при уровне значимости 0,1.
Задача 3053. Два токарных станка изготовляют детали по одному чертежу. Из продукции первого станка было отобрано деталей, а из продукции второго деталей. Выборочные дисперсии контрольно размера, определенные по этим выборкам, равны соответственно 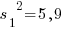 мкм2 и
мкм2 и 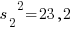 мкм2. Проверить гипотезу о равенстве дисперсий при α=0,05, если альтернативная гипотеза утверждает, что дисперсии не равны.
мкм2. Проверить гипотезу о равенстве дисперсий при α=0,05, если альтернативная гипотеза утверждает, что дисперсии не равны.
Задача 3054. На двух станках производят одну и ту же продукцию, контролируемую по наружному диаметру изделия. Из продукции станка А было проверено 16 изделий, а из продукции станка В – 25 изделий. Выборочные оценки математических ожиданий и дисперсий контролируемых размеров составили 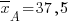 мм при
мм при 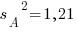 мм2 и
мм2 и 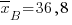 мм при
мм при 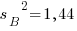 мм2. Проверить гипотезу о равенстве дисперсий, если α=0,1.
мм2. Проверить гипотезу о равенстве дисперсий, если α=0,1.
Задача 3055. На двух станках с программным управлением обрабатываются одинаковые детали. Для оценки точности станков отобраны 10 деталей с первого станка и 12 деталей со второго станка. По этим выборкам найдены исправленные выборочные дисперсии, равные соответственно 30 кв. ед. и 10 кв. ед. Можно ли на основании этих данных утверждать на 5% уровне значимости, что дисперсии существенно различны, а следовательно имеются значительные различия в точности станков?
Задача 3056. Ожидается, что добавление специальных веществ уменьшает жесткость воды. Оценки жесткости воды до и после добавления реагента по 40 и 50 пробам соответственно показали средние значения жесткости равны 4,9 и 3,8 град (в градусах жесткости). Дисперсия измерений в обоих случаях предполагается известной и равной 0,25 град2. Подтверждают ли эти результаты ожидаемый эффект? При расчетах положить α=0,05.
Задача 3057. Для проверки эффективности новой технологии отобраны две группы рабочих: в первой группе численностью 70 человек при старой технологии средняя выработка оставила 78 изделий, во второй группе из 50 человек при новой технологии средняя выработка составила 85 изделий. Предварительно установлено (известно), что дисперсии выработки в группах соответственно равны 74 и 100. При уровне значимости 0,05 выяснить влияние новой технологии на среднюю производительность.
Задача 3058. Поступление страховых взносов в 130 филиалов страховых организаций в регионе А составило 2704 у.е., в В на 100 филиалов пришлось 1872 у.е. Дисперсия величины страховых взносов в регионе А равна 4212 (у.е.2), в регионе В - 2625 (у.е.2). На уровне значимости α=0,05 определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на один филиал.
Задача 3059. Для сравнения точности двух станков - автоматов взяты выборки объёмом соответственно 12 и 10 деталей. По результатам измерения контролируемого размера вычислены выборочные средние (100 мм и 102 мм) и выборочные дисперсии, которые соответственно равны 4.05 и 2.85 мм2. На уровне значимости 0,05 проверить гипотезу о том, что генеральные средние обеих совокупностей равны против конкурирующей гипотезы о том, что генеральная средняя второй совокупности больше первой.
Задача 3060. На коробках с конфетами было подготовлено два варианта рисунка. В течение тридцати дней ежедневно регистрировалось число проданных коробок каждого вида, которое колебалось от 0 до 8, по заданной таблице при уровне значимости 0,05 ответить на вопрос - повлиял ли рисунок на объём продаж (первая строка таблицы – число проданных коробок, вторая и третья строки – количество дней с данным объёмом продаж соответственно коробок первого и второго типа).
0 1 2 3 4 5 6 7 8
-------------------------
3 3 5 5 5 4 3 1 1
------------------------
0 2 3 5 7 6 3 2 2
Задача 3061. Для изучения влияния курения на продолжительность жизни отслеживалась продолжительность двух групп населения по 100 чел. каждого, курящих и некурящих. Пользуясь таблицей, при уровне значимости 0,05 ответить на вопрос, влияет ли курение на продолжительность жизни (первая строка таблицы - число лет, вторая и третья число человек проживающих число лет соответственно в группах курящих не курящих)
20 30 40 50 60 70 80 90
0 10 20 30 30 5 4 1
0 5 15 25 35 10 10 0
Задача 3062. Для испытания шерстяной ткани на прочность произведены две выборки объемами пх = 40 и ny = 30. Средняя прочность оказалась равной 135 г и 138 г. Предварительные исследования показали, что прочность шерстяной ткани в генеральных совокупностях Х и Y имеют нормальное распределение с дисперсиями 20 и 35. При уровне значимости 0,01 определить существенность расхождения между средними в обеих выборках.
Задача 3063. Статистическая обработка результатов анализа вещества на содержание некоторого компонента двумя различными методами показала следующее. В случае использования первого метода при анализе 7 образцов вещества получена средняя величина содержания компонента, равная 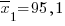 , при исправленной выборочной дисперсии
, при исправленной выборочной дисперсии 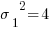 ; при анализе 8 образцов вторым методом соответствующие характеристики оказались равными
; при анализе 8 образцов вторым методом соответствующие характеристики оказались равными 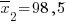 и
и 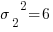 . В предположении нормальности распределения величины содержания компонента при использовании каждого из этих двух методов анализа при уровне значимости p = 0,05 проверить: позволяют ли проведенные исследования утверждать, что результаты анализа зависят от используемого метода?
. В предположении нормальности распределения величины содержания компонента при использовании каждого из этих двух методов анализа при уровне значимости p = 0,05 проверить: позволяют ли проведенные исследования утверждать, что результаты анализа зависят от используемого метода?
Задача 3064. Кондитерская компания решила выяснить, действительно ли новая упаковка увеличивает объем продаж дорогих конфет. Исследования были проведены в 35 магазинах и супермаркетах, продающих конфеты в старой упаковке и 42 магазинах, в которых продавались конфеты в новой упаковке. Среднедневной объем продаж конфет в старой упаковке составил 27,4 коробки с дисперсией 6,8, а объем продаж конфет в новой упаковке составил 35,6 с дисперсией 4,2. Можно ли на уровне значимости α=0,01 утверждать, что новая упаковка увеличивает объем продаж конфет?
Задача 3065. Два лаборанта проводили определение меди в воде методом йодометрического титрования. Было выполнено по 3 параллельных определения. Первый лаборант получил среднее значение 22,0 мг/л, дисперсия составила 0,04, второй лаборант – 21,3 мг/л, дисперсия составила 0,02. Можно ли объединить результаты лаборантов в одну выборку?
Задача 3066. Для двух городов по независимым выборкам объемов n1=60 и n2=50 найдены средний возраст 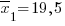 и
и 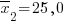 нарушителя уголовного законодательства и дисперсия
нарушителя уголовного законодательства и дисперсия 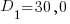 и
и 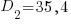 возраста нарушителя. Значимо ли различие средних? Принять уровень значимости равным α=0,05 .
возраста нарушителя. Значимо ли различие средних? Принять уровень значимости равным α=0,05 .
* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.
