Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.
Классическое определение вероятности: список решений задач
Ниже даны ссылки на страницы с текстами задач на тему "Классическое определение вероятности". Все задачи имеют полное и качественное решение.
Классическое определение вероятности: теория и задачи
Основным понятием теории вероятностей является понятие случайного события. Случайное событие - это событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, выпадение двух гербов или герба и решки при бросании двух монет - это случайные события.
Сначала введем некоторые определения, касающиеся случайных событий: достоверные, невозможные, несовместные события.
Достоверное событие - то, которое в результате испытания обязательно происходит. Например, "выпадет или орел, или решка при бросании одной монеты".
Невозможное событие то, которое в результате испытания произойти не может. Например, "вытащен красный шар из ящика, в котором 3 белых и 3 черных шара".
Несовместные случайные события - такие, что никакие два из них не могут появиться вместе в данном испытании. Например "выпадение герба" и "выпадение решки" при испытании, состоящем в бросании одной монеты
Случайные события образуют полную группу событий, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Таким образом, эти события покрывают все возможные исходы испытания.
Перейдем к определению классической вероятности. Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.
Пример. В мешке находится 10 пронумерованных бочонков (на каждом бочонке поставлено по одной цифре от 1 до 10). Бочонки с цифрами 1, 2, 3 и 4 - красные, остальные – черные. Появление бочонка с цифрой 1 (или цифрой 2, или цифрой 3, или цифрой 4) есть событие, благоприятствующее появлению красного бочонка. Появление бочонка с цифрой 4 (или цифрой 5, 6, 7, 8, 9, 10) есть событие, благоприятствующее появлению черного бочонка.
Вероятностью события A называют отношение числа благоприятствующих этому событию исходов m к общему числу всех равновозможных несовместных элементарных исходов n, образующих полную группу исходов: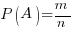 
. Это классическое определение вероятности.
Перечислим свойства вероятности:
1. Вероятность достоверного события равна единице
2. Вероятность невозможного события равна нулю.
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Таким образом, вероятность любого события удовлетворяет неравенству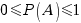 
.
Приведем несколько решений примеров на классическое определение вероятности.
Пример. В урне 10 пронумерованных бочонков с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого бочонка не превосходит 2?
Решение. Пусть событие А = (Номер вынутого бочонка не превосходит 2). Число случаев благоприятствующих появлению события А равно числу бочонков с номерами не более 2 (то есть 1 и 2), поэтому m=2. Общее число исходов n=10. Следовательно,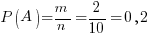 
.
Пример. На входной двери имеется замок c 10 цифрами на кнопках. Для того, чтобы открыть замок, необходимо нажать три кнопки так, чтобы цифры на них составили определенное число. Найти вероятность того, что замок откроют с первой попытки.
Решение. Найдем вероятность этого события по классическому определению вероятности: 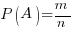, где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных исходов.
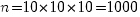- число различных кодовых комбинаций (первая цифра любая от 0 до 9, вторая цифра любая от 0 до 9 и третья цифра любая от 0 до 9).
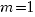- только одна комбинация (число) верная.
Тогда вероятность открыть замок равна: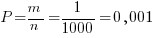 
.
Другие примеры задач по классической вероятности вы найдете на странице Примеры по теории вероятностей.