Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.
Полная вероятность и формула Байеса: список решений задач
Ниже даны ссылки на страницы с текстами задач на тему "Полная вероятность и формула Байеса". Все задачи имеют полное и качественное решение.
Полная вероятность и формула Байеса: теория и задачи
Пусть событие А может произойти при выполнении одного из несовместных событий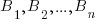 
. Если эти события (их еще называют гипотезами) образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле полной вероятности: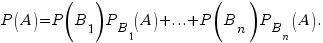 
Если событие А произошло, то это может изменить вероятности гипотез B_1, B_2, ..., B_n",$size,$pathtoimg); ?>, которые вычисляются по формуле Байеса (формуле Бейеса): 
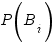называются априорными вероятностями. Вероятности этих событий в предположении, что А наступило - 
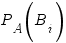- апостериорными вероятностями.
Пример. В магазин привозят товары от трех поставщиков: первый привозит 20%, второй - 30% и третий - 50% всего поступающего товара. Известно, что 10% товара первого поставщика высшего сорта, для второго и третьего поставщика эти значения равны 5% и 20%. Найти вероятность того, что случайно выбранный товар окажется высшего сорта.
Решение. Обозначим через A событие, заключающееся в том, что будет выбран товар высшего сорта. Введем гипотезы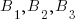 
, заключающиеся в выборе товара, поступившего соответственно от первого, второго и третьего поставщика. По условию известно, что
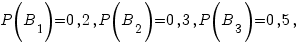
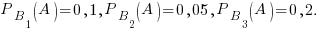
Применяем формулу полной вероятности:
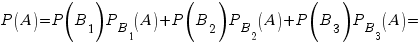
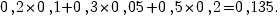
Пример. В условиях предыдущей задачи найти вероятность того, что товар был привезен первым поставщиком, если он оказался высшего сорта.
Решение. Сохраним обозначения предыдущей задачи (см. выше). Тогда нужно вычислить апостериорную вероятность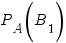 
. Используем формулу Байеса: 
Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.