Вы можете использовать данную форму поиска, чтобы найти нужную задачу. Вводите слово, фразу из задачи или ее номер, если он вам известен.
Геометрическая вероятность: список решений задач
Ниже даны ссылки на страницы с текстами задач на тему "Геометрическая вероятность". Все задачи имеют полное и качественное решение.
Геометрическая вероятность: теория и задачи
Не всегда бывает удобно для непосредственного подсчета вероятности использовать классическое определение вероятности (например, когда число исходов некоторого опыта бесконечно, как при выборе точки из отрезка и т.п.). Зачастую при этом используется другой метод - геометрический подход к определению вероятности.
Предположим, что случайное испытание можно представить как бросание произвольной точки наудачу в некоторую геометрическую область D (на прямой, плоскости или пространстве, в зависимости от задачи).
Элементарные исходы – это отдельные точки области D, любое событие – это некоторое подмножество этой области (фактически - пространства элементарных исходов). Можно считать, что все точки D "равноправны", и тогда вероятность попадания точки в некоторое подмножество этой области пропорциональна мере (длине, площади, объему) подмножества и не зависит от его расположения внутри области и формы. Таким образом приходим к геометрическому определению вероятности.
Геометрическая вероятность некоторого события А определяется формулой:
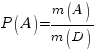
Здесь  – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и множества исходов, благоприятствующих осуществлению события А.
– геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и множества исходов, благоприятствующих осуществлению события А.
Пример. Мишень для выстрелов в тире представляет собой круг радиуса R. Стрелок выбивает 10 очков, если попадает в малый круг в центре с радиусом r, 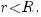 Какова вероятность выбить 10 очков при одном выстреле?
Какова вероятность выбить 10 очков при одном выстреле?
Решение. Используем геометрическое определение вероятности. Множество всех элементарных исходов - мишень, круг радиуса R, его площадь равна 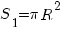 . Множество элементарных исходов, соответствующих событию "Выбито 10 очков" - это круг радиуса rего площадь равна
. Множество элементарных исходов, соответствующих событию "Выбито 10 очков" - это круг радиуса rего площадь равна 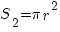 .
.
По геометрическому определению вероятности получаем, что искомая вероятность есть отношение площади малого круга, куда пуля должна попасть, к площади всей мишени - большого круга, то есть: 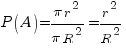 .
.
Пример. На плоскость, расчерченную параллельными полосками шириной в 2d (расстояние между осевыми линиями равно 2D), наудачу брошен круг радиуса r 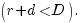 Найти вероятность того, что данный круг пересечет некоторую полоску (линию).
Найти вероятность того, что данный круг пересечет некоторую полоску (линию).
Решение. Положим, что элементарный исход испытания - это расстояние x от центра круга до осевой линии ближайшей к кругу полоски. Тогда все пространство элементарных исходов – это отрезок 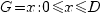 . Пересечение круга с полоской произойдет только в том случае, если его центр попадет в полосу, т.е.
. Пересечение круга с полоской произойдет только в том случае, если его центр попадет в полосу, т.е. 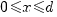 , или будет находится от края полосы на расстоянии меньшем чем радиус, т.е.
, или будет находится от края полосы на расстоянии меньшем чем радиус, т.е. 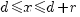 .
.
По геометрическому определению вероятности получаем ответ: 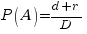 .
.
Другие примеры задач по теории вероятности вы найдете на странице Примеры по теории вероятностей.
